题目内容
已知数列{an}满足an•an-2=an-1(n>2,n∈N),且a1=2,a2=3,则a2013= .
【答案】分析:利用已知计算得出an+6=a1是解题的关键.
解答:解:∵数列{an}满足an•an-2=an-1(n>2,n∈N),且a1=2,a2=3,∴a3•a1=a2,解得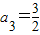 ,
,
a4•a2=a3,解得a4= ,
,
a5•a3=a4,解得a5= .
.
a6•a4=a5,解得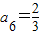 .
.
a7•a5=a6,解得a7=2.
….
∴an+6=a1.
∴a2013=a335×6+3=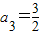 .
.
故答案为 .
.
点评:利用已知得出其周期性是解题的关键.
解答:解:∵数列{an}满足an•an-2=an-1(n>2,n∈N),且a1=2,a2=3,∴a3•a1=a2,解得
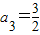 ,
,a4•a2=a3,解得a4=
 ,
,a5•a3=a4,解得a5=
 .
.a6•a4=a5,解得
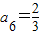 .
.a7•a5=a6,解得a7=2.
….
∴an+6=a1.
∴a2013=a335×6+3=
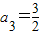 .
.故答案为
 .
.点评:利用已知得出其周期性是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目