题目内容
14.设两向量e1、e2满足|${\overrightarrow{e}}_{1}$|=2,|${\overrightarrow{e}}_{2}$|=1,${\overrightarrow{e}}_{1}$、${\overrightarrow{e}}_{2}$的夹角为60°,若向量2t${\overrightarrow{e}}_{1}$+7${\overrightarrow{e}}_{2}$与向量${\overrightarrow{e}}_{1}$+t${\overrightarrow{e}}_{2}$的夹角为[0,$\frac{π}{2}$),求实数t的取值范围.分析 两向量e1、e2满足|${\overrightarrow{e}}_{1}$|=2,|${\overrightarrow{e}}_{2}$|=1,${\overrightarrow{e}}_{1}$、${\overrightarrow{e}}_{2}$的夹角为60°,不妨设$\overrightarrow{{e}_{2}}$=(1,0),$\overrightarrow{{e}_{1}}$=$(1,\sqrt{3})$,可得2t${\overrightarrow{e}}_{1}$+7${\overrightarrow{e}}_{2}$,${\overrightarrow{e}}_{1}$+t${\overrightarrow{e}}_{2}$,由于向量2t${\overrightarrow{e}}_{1}$+7${\overrightarrow{e}}_{2}$与向量${\overrightarrow{e}}_{1}$+t${\overrightarrow{e}}_{2}$的夹角为[0,$\frac{π}{2}$),可得(2t${\overrightarrow{e}}_{1}$+7${\overrightarrow{e}}_{2}$)(${\overrightarrow{e}}_{1}$+t${\overrightarrow{e}}_{2}$)=(2t+7)(t+1)+21t>0,解出即可得出.
解答 解:∵两向量e1、e2满足|${\overrightarrow{e}}_{1}$|=2,|${\overrightarrow{e}}_{2}$|=1,${\overrightarrow{e}}_{1}$、${\overrightarrow{e}}_{2}$的夹角为60°,
不妨设$\overrightarrow{{e}_{2}}$=(1,0),$\overrightarrow{{e}_{1}}$=$(1,\sqrt{3})$,
则2t${\overrightarrow{e}}_{1}$+7${\overrightarrow{e}}_{2}$=(2t+7,7$\sqrt{3}$),${\overrightarrow{e}}_{1}$+t${\overrightarrow{e}}_{2}$=$(t+1,t\sqrt{3})$.
∵向量2t${\overrightarrow{e}}_{1}$+7${\overrightarrow{e}}_{2}$与向量${\overrightarrow{e}}_{1}$+t${\overrightarrow{e}}_{2}$的夹角为[0,$\frac{π}{2}$),
∴向量(2t${\overrightarrow{e}}_{1}$+7${\overrightarrow{e}}_{2}$)(${\overrightarrow{e}}_{1}$+t${\overrightarrow{e}}_{2}$)=(2t+7)(t+1)+21t>0,
化为2t2+30t+7>0,
解得t>$\frac{-15+\sqrt{211}}{2}$或t<$\frac{-15-\sqrt{211}}{2}$.
∴实数t的取值范围是t>$\frac{-15+\sqrt{211}}{2}$或t<$\frac{-15-\sqrt{211}}{2}$.
点评 本题考查了向量的坐标运算、向量夹角公式、数量积运算性质,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案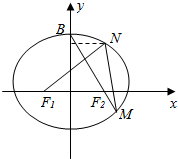 如图,已知F1、F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,顶点B的坐标是(0,b),连接BF2并延长交椭圆于点M,点M关于x轴的对称点为N,连接F1、N.
如图,已知F1、F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,顶点B的坐标是(0,b),连接BF2并延长交椭圆于点M,点M关于x轴的对称点为N,连接F1、N.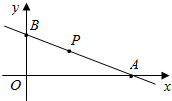 直线l过点P(2,3)且分别与x、y正半轴于A,B两点,O为原点.
直线l过点P(2,3)且分别与x、y正半轴于A,B两点,O为原点.