题目内容
【题目】设a为实数,函数f(x)=![]() +a
+a![]() +a
+a![]() .
.
(1)设t=![]() ,求t的取值范图;
,求t的取值范图;
(2)把f(x)表示为t的函数h(t);
(3)设f (x)的最大值为M(a),最小值为m(a),记g(a)=M(a)-m(a)求g(a)的表达式.
【答案】(1)[![]() ,2]; (2)h(t)=at+
,2]; (2)h(t)=at+![]() ,
,![]() ≤t≤2; (3)g(a)=
≤t≤2; (3)g(a)=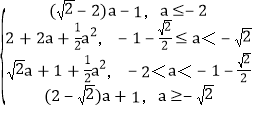 ..
..
【解析】
(1)将t=![]() 两边平方,结合二次函数的性质可得t的范围;(2)由(1)可得
两边平方,结合二次函数的性质可得t的范围;(2)由(1)可得![]() =
=![]() ,可得h(t)的解析式;(3)求得h(t)=
,可得h(t)的解析式;(3)求得h(t)=![]() (t+a)2-1-
(t+a)2-1-![]() a2,对称轴为t=-a,讨论对称轴与区间[
a2,对称轴为t=-a,讨论对称轴与区间[![]() ,2]的关系,结合单调性可得h(t)的最值,即可得到所求g(a)的解析式.
,2]的关系,结合单调性可得h(t)的最值,即可得到所求g(a)的解析式.
(1)t=![]() ,可得t2=2+2
,可得t2=2+2![]() ,
,
由0≤1-x2≤1,可得2≤t2≤4,
又t≥0可得![]() ≤t≤2,
≤t≤2,
即t的取值范围是[![]() ,2];
,2];
(2)由(1)可得![]() =
=![]() ,
,
即有h(t)=at+![]() ,
,![]() ≤t≤2;
≤t≤2;
(3)由h(t)=![]() (t+a)2-1-
(t+a)2-1-![]() a2,
a2,
对称轴为t=-a,
当-a≥2即a≤-2时,h(t)在[![]() ,2]递减,
,2]递减,
可得最大值M(a)=h(![]() )=
)=![]() a;最小值m(a)=h(2)=1+2a,
a;最小值m(a)=h(2)=1+2a,
则g(a)=(![]() -2)a-1;
-2)a-1;
当-a≤![]() 即a≥-
即a≥-![]() 时,h(t)在[
时,h(t)在[![]() ,2]递增,
,2]递增,
可得最大值M(a)=h(2)=1+2a;最小值m(a)=h(![]() )=
)=![]() a,
a,
则g(a)=(2-![]() )a+1;
)a+1;
当![]() <-a<2即-2<a<-
<-a<2即-2<a<-![]() 时,h(t)的最小值为m(a)=h(-a)=-1-
时,h(t)的最小值为m(a)=h(-a)=-1-![]() a2,
a2,
若-1-![]() ≤a<-
≤a<-![]() ,则h(2)≥h(
,则h(2)≥h(![]() ),可得h(t)的最大值为M(a)=h(2)=1+2a,
),可得h(t)的最大值为M(a)=h(2)=1+2a,
可得g(a)=2+2a+![]() a2;
a2;
若-2<a<-1-![]() ,则h(2)<h(
,则h(2)<h(![]() ),可得h(t)的最大值为M(a)=h(
),可得h(t)的最大值为M(a)=h(![]() )=
)=![]() a,
a,
可得g(a)=![]() a+1+
a+1+![]() a2;
a2;
综上可得g(a)=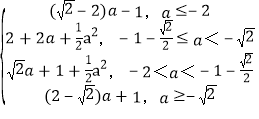 .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
