题目内容
已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点P(4,m)到焦点的距离为6.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线y=kx-2相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线y=kx-2相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
分析:(Ⅰ)由题意设:抛物线方程为y2=2px,其准线方程为x=-
,根据抛物线的大于可得:4+
=6 ,进而得到答案.(Ⅱ)联立直线与抛物线的方程得 k2x2-(4k+8)x+4=0,根据题意可得△=64(k+1)>0即k>-1且k≠0,再结合韦达定理可得k的值.
| p |
| 2 |
| p |
| 2 |
解答:解:(Ⅰ)由题意设抛物线方程为y2=2px,其准线方程为x=-
,
∵P(4,m)到焦点的距离等于A到其准线的距离,
∴4+
=6 ∴p=4
∴抛物线C的方程为y2=8x
(Ⅱ)由
消去y,得 k2x2-(4k+8)x+4=0
∵直线y=kx-2与抛物线相交于不同两点A、B,则有k≠0,△=64(k+1)>0,解得k>-1且k≠0,
又
=
=2,
解得 k=2,或k=-1(舍去)
∴k的值为2.
| p |
| 2 |
∵P(4,m)到焦点的距离等于A到其准线的距离,
∴4+
| p |
| 2 |
∴抛物线C的方程为y2=8x
(Ⅱ)由
|
∵直线y=kx-2与抛物线相交于不同两点A、B,则有k≠0,△=64(k+1)>0,解得k>-1且k≠0,
又
| x1+x2 |
| 2 |
| 2k+4 |
| k2 |
解得 k=2,或k=-1(舍去)
∴k的值为2.
点评:本题主要考查抛物线的标准方程,以及直线与抛物线的位置关系.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
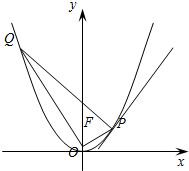 已知抛物线C的顶点在原点,焦点为F(0,1).
已知抛物线C的顶点在原点,焦点为F(0,1).