题目内容
已知函数y=f(x)是定义在R上且以3为周期的奇函数,当x∈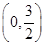 时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
| A.3 | B.5 | C.7 | D.9 |
C
解析

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
已知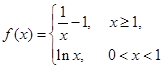 ,若
,若 恒成立,则
恒成立,则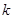 的取值范围是( )
的取值范围是( )
A.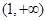 | B.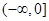 | C.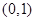 | D. |
定义运算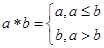 ,如
,如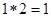 ,令
,令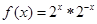 ,则
,则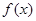 为( )
为( )
A.奇函数,值域 | B.偶函数,值域 |
C.非奇非偶函数,值域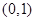 | D.偶函数,值域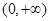 |
已知函数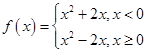 .若
.若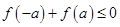 ,则
,则 的取值范围是( )
的取值范围是( )
A.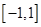 | B.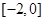 | C.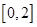 | D. |
函数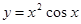 部分图象可以为( )
部分图象可以为( )
A.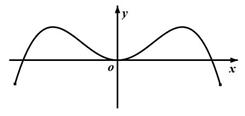 |
B.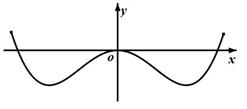 |
C.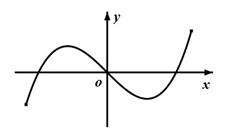 |
D.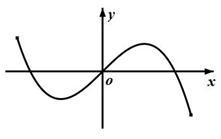 |
已知函数 ,若
,若 ,
, 为某一个三角形的边长,则实数m的取值范围是( )
为某一个三角形的边长,则实数m的取值范围是( )
A. | B. | C. | D. |
已知定义域为R的函数f(x)满足:f(4)=-3,且对任意x∈R总有f′(x)<3,则不等式f(x)<3x-15的解集为( )
| A.(-∞,4) |
| B.(-∞,-4) |
| C.(-∞,-4)∪(4,+∞) |
| D.(4,+∞) |
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )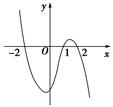
| A.函数f(x)有极大值f(2)和极小值f(1) |
| B.函数f(x)有极大值f(-2)和极小值f(1) |
| C.函数f(x)有极大值f(2)和极小值f(-2) |
| D.函数f(x)有极大值f(-2)和极小值f(2) |
若f(x+1)=2f(x),则f(x)等于( )
| A.2x | B.2x | C.x+2 | D.log2x |