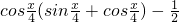题目内容
设函数y=f(x)满足:对任意的实数x∈R,有f(sinx)=-cos2x+cos2x+2sinx-3.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若方程f(x)=2a|x-
|有解,求实数a的取值范围.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若方程f(x)=2a|x-
| 1 |
| 2 |
(Ⅰ)f(sinx)=2sin2x-1+1-sin2x+2sinx-3=sin2x+2sinx-3,
所以f(x)=x2+2x-3(-1≤x≤1).
(Ⅱ)①当x=
时,f(
)≠0,不成立.
②当-1≤x<
时,x-
<0,
令t=
-x,则x=
-t,0<t≤
,2a=
=t-
-3,
因为函数h(t)=t-
-3在(0,
]上单增,所以2a≤h(
)=-
?a≤-
.
③当
<x≤1时,x-
>0,
令t=x-
,则x=
+t,0<t≤
,2a=
=t-
+3,
因为函数g(t)=t-
+3在(0,
]上单增,所以2a≤g(
)=0?a≤0.
综上,实数a的取值范围是(-∞,0].
所以f(x)=x2+2x-3(-1≤x≤1).
(Ⅱ)①当x=
| 1 |
| 2 |
| 1 |
| 2 |
②当-1≤x<
| 1 |
| 2 |
| 1 |
| 2 |
令t=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(
| ||||
| t |
| 7 |
| 4t |
因为函数h(t)=t-
| 7 |
| 4t |
| 3 |
| 2 |
| 3 |
| 2 |
| 8 |
| 3 |
| 4 |
| 3 |
③当
| 1 |
| 2 |
| 1 |
| 2 |
令t=x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(
| ||||
| t |
| 7 |
| 4t |
因为函数g(t)=t-
| 7 |
| 4t |
| 1 |
| 2 |
| 1 |
| 2 |
综上,实数a的取值范围是(-∞,0].

练习册系列答案
相关题目