题目内容
计算以下定积分:(1)
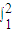 (2x2-
(2x2-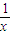 )dx;
)dx;(2)
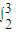 (
(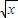 +
+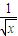 )2dx;
)2dx;(3)
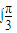 (sinx-sin2x)dx.
(sinx-sin2x)dx.
【答案】分析:(1)求出被积函数2x2-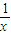 的原函数,将积分的上限、下限代入求值.
的原函数,将积分的上限、下限代入求值.
(2)先化简被积函数,然后求出被积函数x+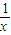 +2的原函数,将积分的上限、下限代入求值.
+2的原函数,将积分的上限、下限代入求值.
(3)先求出sinx-sin2x的原函数,然后利用微积分基本定理,∫abf(x)±g(x)dx=∫abf(x)dx±∫abg(x)dx求出值.
解答:解:(1)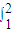 (2x2-
(2x2-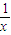 )dx=(
)dx=( x3-lnx)
x3-lnx)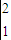
=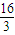 -ln2-
-ln2- =
= -ln2.
-ln2.
(2)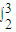 (
(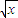 +
+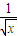 )2dx=
)2dx=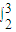 (x+
(x+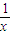 +2)dx
+2)dx
=( x2+lnx+2x)
x2+lnx+2x)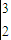
=( +ln3+6)-(2+ln2+4)
+ln3+6)-(2+ln2+4)
=ln +
+ .
.
(3)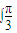 (sinx-sin2x)dx=(-cosx+
(sinx-sin2x)dx=(-cosx+ cos2x)
cos2x)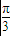
=(- -
- )-(-1+
)-(-1+ )=-
)=- .
.
点评:本题主要考查了定积分的计算,解决该类问题的关键是求出被积函数的原函数,属于计算题、基础题.
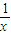 的原函数,将积分的上限、下限代入求值.
的原函数,将积分的上限、下限代入求值.(2)先化简被积函数,然后求出被积函数x+
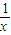 +2的原函数,将积分的上限、下限代入求值.
+2的原函数,将积分的上限、下限代入求值.(3)先求出sinx-sin2x的原函数,然后利用微积分基本定理,∫abf(x)±g(x)dx=∫abf(x)dx±∫abg(x)dx求出值.
解答:解:(1)
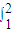 (2x2-
(2x2-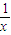 )dx=(
)dx=( x3-lnx)
x3-lnx)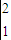
=
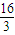 -ln2-
-ln2- =
= -ln2.
-ln2.(2)
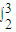 (
(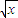 +
+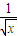 )2dx=
)2dx=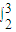 (x+
(x+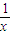 +2)dx
+2)dx=(
 x2+lnx+2x)
x2+lnx+2x)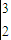
=(
 +ln3+6)-(2+ln2+4)
+ln3+6)-(2+ln2+4)=ln
 +
+ .
.(3)
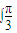 (sinx-sin2x)dx=(-cosx+
(sinx-sin2x)dx=(-cosx+ cos2x)
cos2x)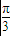
=(-
 -
- )-(-1+
)-(-1+ )=-
)=- .
.点评:本题主要考查了定积分的计算,解决该类问题的关键是求出被积函数的原函数,属于计算题、基础题.

练习册系列答案
相关题目