题目内容
投掷骰子两次,第一次出现点数是a,第二次出现点数是b,求方程组
|
(Ⅰ)有惟一解的概率;
(Ⅱ)x、y都是正数解的概率.
分析:(I)利用分布计数原理求出骰子投掷2次所有的结果,通过解二元一次方程组判断出方程组有唯一解的条件,先求出不满足条件结果个数,再求出方程组有唯一解的结果个数,利用古典概型的概率公式求出方程组只有一个解的概率.
(II)首先列举出a,b所有的可能结果,然后求出有正整数解时,列举出所有的可能事件,进而求出概率.
(II)首先列举出a,b所有的可能结果,然后求出有正整数解时,列举出所有的可能事件,进而求出概率.
解答:解:(Ⅰ)骰子投掷2次所有的结果有6×6=36
由
得(b-2a)y=3-2a
当b-2a≠0时,方程组有唯一解
当b=2a时包含的结果有:
当a=1时,b=2
当a=2时,b=4
当a=3时,b=6共三个
所以方程组只有一个解包含的基本结果有36-3=33
由古典概型的概率公式得
=
故答案为:
(Ⅱ)解方程组得
当
或
时x>0且y>0 (9分)
即
或
时,x>0且y>0,则当b=1或2时,a=2,3,4,5,6;
当b=4或5或6时,a=1.
所以P(A)=
. (12分)
由
|
当b-2a≠0时,方程组有唯一解
当b=2a时包含的结果有:
当a=1时,b=2
当a=2时,b=4
当a=3时,b=6共三个
所以方程组只有一个解包含的基本结果有36-3=33
由古典概型的概率公式得
| 33 |
| 36 |
| 11 |
| 12 |
故答案为:
| 11 |
| 12 |
(Ⅱ)解方程组得
|
|
|
即
|
|
当b=4或5或6时,a=1.
所以P(A)=
| 13 |
| 36 |
点评:本题考查古典概型,考查解方程组,是一个综合题,概率问题往往同其他的知识点结合在一起,实际上是以概率问题为载体,主要考查的是另一个知识点.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 ,第二次向上的点数记为
,第二次向上的点数记为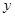 ,在直角坐标系
,在直角坐标系 中,以
中,以 为坐标的点落在直线
为坐标的点落在直线 上的概率为 ( )
上的概率为 ( )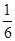 B.
B. C.
C. D.
D.