题目内容
函数 在区间 上单调递减(
)
在区间 上单调递减(
)
A. B.(-
B.(- C.
C. D.
D.
【答案】
D
【解析】
试题分析:
 ,令
,令 ,
,
解得 ,令
,令 得函数在
得函数在 上单调递增.
上单调递增.
考点:本小题主要考查两角和与差的正弦、余弦公式、辅助角公式的应用和由三角函数图象考查三角函数的性质,考查学生的运算求解能力和数形结合分析问题、解决问题的能力.
点评:要考查三角函数的性质,必须化成 的形式,然后借助三角函数的图象解决,还需要注意的是本题的
的形式,然后借助三角函数的图象解决,还需要注意的是本题的 只是所求出的单调区间的一部分,并不是完整的一个单调区间.
只是所求出的单调区间的一部分,并不是完整的一个单调区间.

练习册系列答案
相关题目
已知函数 ,(
,( ),
),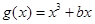
(1)若曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当 时,若函数
时,若函数 的单调区间,并求其在区间(-∞,-1)上的最大值。
的单调区间,并求其在区间(-∞,-1)上的最大值。
【解析】(1) ,
,
∵曲线 与曲线
与曲线 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴ ,
,
∴
(2)令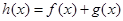 ,当
,当 时,
时,
 令
令 ,得
,得
 时,
时,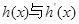 的情况如下:
的情况如下:
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函数 的单调递增区间为
的单调递增区间为 ,
, ,单调递减区间为
,单调递减区间为
当 ,即
,即 时,函数
时,函数 在区间
在区间 上单调递增,
上单调递增, 在区间
在区间 上的最大值为
上的最大值为 ,
,
当 且
且 ,即
,即 时,函数
时,函数 在区间
在区间 内单调递增,在区间
内单调递增,在区间 上单调递减,
上单调递减, 在区间
在区间 上的最大值为
上的最大值为
当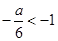 ,即a>6时,函数
,即a>6时,函数 在区间
在区间 内单调递赠,在区间
内单调递赠,在区间 内单调递减,在区间
内单调递减,在区间 上单调递增。又因为
上单调递增。又因为
所以 在区间
在区间 上的最大值为
上的最大值为 。
。
 ,②
,② ,③
,③ ,④
,④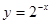 ,其中在区间[0,+
,其中在区间[0,+ )上单调递
)上单调递


