题目内容
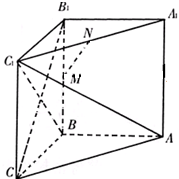 如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=CC1,M、N分别为BB1、A1C1的中点.
如图所示,在直三棱柱ABC-A1B1C1中,∠ABC=90°,BC=CC1,M、N分别为BB1、A1C1的中点.(Ⅰ)求证:CB1⊥平面ABC1;
(Ⅱ)求证:MN∥平面ABC1.
分析:(I)根据直三棱柱的性质,利用面面垂直性质定理证出AB⊥平面BB1C1,得出AB⊥CB1.正方形BCC1B1中,对角线CB1⊥BC1,由线面垂直的判定定理可证出CB1⊥平面ABC1;
(II)取AC1的中点F,连BF、NF,利用三角形中位线定理和平行四边形的性质,证出EF∥BM且EF=BM,从而得到BMNF是平行四边形,可得MN∥BF,结合线面平行判定定理即可证出MN∥面ABC1.
(II)取AC1的中点F,连BF、NF,利用三角形中位线定理和平行四边形的性质,证出EF∥BM且EF=BM,从而得到BMNF是平行四边形,可得MN∥BF,结合线面平行判定定理即可证出MN∥面ABC1.
解答:解:(Ⅰ)在直三棱柱ABC-A1B1C1中,
侧面BB1C1C⊥底面ABC,且侧面BB1C1C∩底面ABC=BC,
∵∠ABC=90°,即AB⊥BC,
∴AB⊥平面BB1C1 …(2分)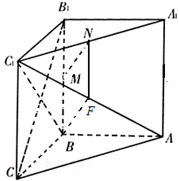
∵CB1?平面BB1C1C,∴AB⊥CB1.…(4分)
∵BC=CC1,CC1⊥BC,∴BCC1B1是正方形,
∴CB1⊥BC1,
∵AB∩BC1=B,∴CB1⊥平面ABC1.
(Ⅱ)取AC1的中点F,连BF、NF.…(7分)
在△AA1C1中,N、F是中点,
∴NF
AA1,
又∵正方形BCC1B1中BM
AA1,
∴EF∥BM,且EF=BM…(8分)
故四边形BMNF是平行四边形,可得MN∥BF,…(10分)
∵BF?面ABC1,MN?平面ABC1,
∴MN∥面ABC1…(12分)
侧面BB1C1C⊥底面ABC,且侧面BB1C1C∩底面ABC=BC,
∵∠ABC=90°,即AB⊥BC,
∴AB⊥平面BB1C1 …(2分)

∵CB1?平面BB1C1C,∴AB⊥CB1.…(4分)
∵BC=CC1,CC1⊥BC,∴BCC1B1是正方形,
∴CB1⊥BC1,
∵AB∩BC1=B,∴CB1⊥平面ABC1.
(Ⅱ)取AC1的中点F,连BF、NF.…(7分)
在△AA1C1中,N、F是中点,
∴NF
| ∥ |
. |
| 1 |
| 2 |
又∵正方形BCC1B1中BM
| ∥ |
. |
| 1 |
| 2 |
∴EF∥BM,且EF=BM…(8分)
故四边形BMNF是平行四边形,可得MN∥BF,…(10分)
∵BF?面ABC1,MN?平面ABC1,
∴MN∥面ABC1…(12分)
点评:本题给出底面为直角三角形的直三棱柱,在已知侧棱与底面直角边长相等的情况下证明线面垂直.着重考查了空间直线与平面平行、垂直的判定与性质等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=2,D、E、F分别是AB、AA1、CC1的中点,P是CD上的点.
如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AA1=AC=BC=2,D、E、F分别是AB、AA1、CC1的中点,P是CD上的点. 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF=
如图所示,在直三棱柱ABC-A1B1C1中,底面是∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,点F在线段AA1上,当AF= 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1,AC1⊥平面A1BD,D为AC的中点. 如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AB=BB1=BC,AC1⊥平面A1BD,D为AC的中点.