题目内容
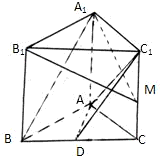已知直三棱柱ABC-A1B1C1的侧棱长与底面三角形的各边长都等于a，D为BC的中点，
（1）求证：A1B∥平面AC1D．
（2）若点M为CC1中点，求证：平面A1B1M⊥平面ADC1
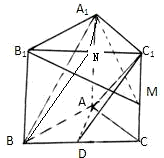证明：（1）法一：连接A1C，与AC1交于点O，连接DO在△A1BC中，A1B∥DO，DO?面AC1D，A1B?面AC1D，∴A1B∥面AC1D
法二：取B1C1中点N，连接A1N，BN∵BN∥C1D，BN?面AC1D∴BN∥面AC1D
又∵A1N∥AD，A1N?面AC1D∴BN∥面AC1D∴面A1BN∥面AC1D∴A1B∥面AC1D
（2）由题意的B1M⊥C1D，由于AD是正三角底边的高线，由直三棱柱ABC-A1B1C1的性质知道：AD与侧面BB1C1C垂直，故有B1M⊥AD，B1M⊥面ADC1∴面A1B1M⊥面ADC1
分析：对于（1），方法一：要证明A1B∥平面AC1D，只需证明A1B与平面AC1D内的一条直线平行即可，故可以连接A1C，与AC1交于点O，容易证明OD为三角形A1BC的中位线，从而得证；
方法二：通过面面平行来转化，取B1C1中点N，连接A1N，可证A1N∥AD，BN∥C1D，通过证明面A1BN∥面AC1D来实现；
对于（2）要证明平面A1B1M⊥平面ADC1，只需证明平面A1B1M内存在一条直线与平面ADC1垂直即可，B1M即可．
点评：本题考查线面平行的判定、面面垂直的判定，要注意期中的转化思想，即将线面平行转化为线线平行、也可以转化为面面平行来证明，将面面垂直转化为线面垂直问题解决．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知直三棱柱ABC-A1B1C1，∠ACB=90°，AC=BC=2，AA1=4．E、F分别是棱CC1、AB中点．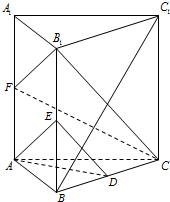
已知直三棱柱ABC-A1B1C1的所有棱长都相等，且D，E，F分别为BC，BB1，AA1的中点．
如图所示，已知直三棱柱ABC-A′B′C′，AC=AB=AA′=2，AC，AB，AA′两两垂直，E，F，H分别是AC，AB，BC的中点，
如图，已知直三棱柱ABC-A1B1C1的侧棱长为2，底面△ABC是等腰直角三角形，且∠ACB=90°，AC=2，D是A A1的中点．
如图，已知直三棱柱ABC-A1B1C1中，AB=AC；M．N．P分别是棱BC．CC1．B1C1的中点．