题目内容
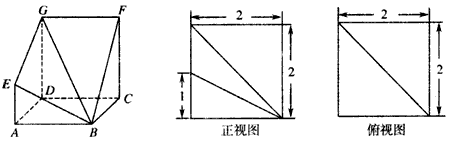
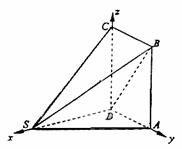
如图,多面体ABCDS中,底面ABCD为矩形,SD⊥AD,SD⊥AB,且AB=2AD,SD=![]() AD,
AD,
(1)求证:平面SDB⊥平面ABCD;
(2)求二面角A―SB―D的大小.

解:(1)∵SD⊥AD,SD⊥AB,AD∩AB=A
∴SD⊥平面ABCD,
又∵SD![]() 平面SBD, ∴平面SDB⊥平面ABCD。
平面SBD, ∴平面SDB⊥平面ABCD。
(2)[解法一]:由(1)知平面SDB⊥平面ABCD,
BD为平面SDB与平面ABCD的交线,过点A作AE⊥DB于E,则AE⊥平面SDB,
又过点A作AF⊥SB于F,连结EF。
由三垂线定理的逆定理得 EF⊥SB,
∴∠AFE为二面角A―SB―D的平面角。
在矩形ABCD中,设AD=a,
则![]() ,
,
在Rt△SBC中,![]()
而在Rt△SAD中,SA=2a,又AB=2a,
∴SB2=SA2+AB2,
即△SAB为等腰直角三角形,且∠SAB为直角,
∴![]()
∴
故二面角A―SB―D的大小为 ![]()
[解法二]:由题可知DS、DA、DC两两互相垂直。
如图建立空间直角坐标系D―xyz
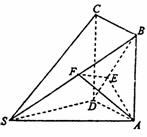
设AD=a,
则S(![]()
![]()
∵![]()
设面SBD的一个法向量为n=(x,y,-1)
则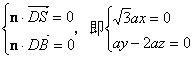
解得 n=(0,2,-1)
又∵ ![]()
设面SAB的一个法向量为m=(1,y,z),
则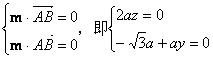
解出 m=(1,![]() ,0),
,0),
![]()
故所求的二面角为arccos![]() 。
。

练习册系列答案
相关题目


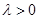 使得
使得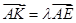 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为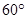 ,求
,求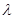 的值。
的值。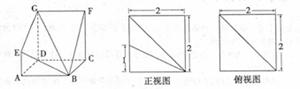
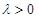 使得
使得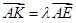 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为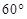 ,求
,求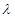 的值。
的值。
 使得
使得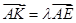 ,二面角A—BG—K的大小为
,二面角A—BG—K的大小为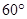 ,求
,求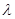 的值。
的值。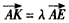 ,KF与平面ABG所成角为30°,求λ的值。
,KF与平面ABG所成角为30°,求λ的值。