题目内容
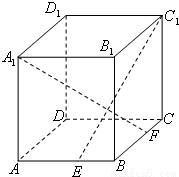
 如图,ABCD-A1B1C1D1是正方体,点E,F分别是BB1,B1D1中点,求证:EF⊥DA1.
如图,ABCD-A1B1C1D1是正方体,点E,F分别是BB1,B1D1中点,求证:EF⊥DA1.分析:建立适当的空间直角坐标系,设正方体棱长为1,求出
,
的坐标,只需证明
•
=0即可.
| DA1 |
| EF |
| DA1 |
| EF |
解答: 解:以
解:以
,
,
分别为x轴,y轴,z轴建立空间直角坐标系,如下图所示:
设正方体棱长为1,则A1(1,0,1),D(0,0,0),F(
,
,1),E(1,1,
),
所以
=(1,0,1),
=(-
,-
,
),
因为
•
=(1,0,1)•(-
,-
,
)=-
+0+
=0,
所以
⊥
,即EF⊥DA1.
 解:以
解:以| DA |
| DC |
| DD1 |
设正方体棱长为1,则A1(1,0,1),D(0,0,0),F(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以
| DA1 |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为
| DA1 |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以
| DA1 |
| EF |
点评:本题考查空间两直线间的垂直关系,考查空间向量在立体几何中的应用,考查学生的运算能力,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
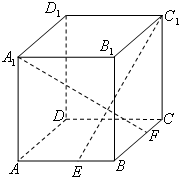 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是