Question

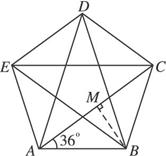
以正五边形ABCDE中A、C为焦点的双曲线经过点D、E，则双曲线的离心率为

 

．

Answer 1

分析：如图所示，建立直角坐标系．设C（2，0）．利用sin18°=

5 -1

4

和正五边形的性质可得：|BC|=

2

cos36°

，又|AD|=2|AE|cos36°=4．利用双曲线的定义可得2a=|AD|-|CD|，即可得出a．再利用e=

c

a

即可得出．

解答：解：如图所示，建立直角坐标系．设C（2，0）．
∵sin18°=

5 -1

4

．
则|BC|=

2

cos36°

=

2

1-2sin218°

=2(

5

-1)．
又|AD|=2|AE|cos36°=4．
∴2a=|AD|-|CD|=4-2(

5

-1)=6-2

5

，∴a=3-

5

，
∴e=

c

a

=

2

3- 5

=

3+ 5

2

．
故答案为

3+ 5

2

．

点评：熟练掌握正五边形的性质、一些角的三角函数值、离心率计算公式等是解题的关键．