题目内容
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() 的坐标满足圆
的坐标满足圆![]() 方程
方程![]() ,且圆心
,且圆心![]() 满足
满足![]() .
.
(1)求椭圆![]() 的方程;
的方程;
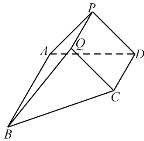
(2)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,过
两点,过![]() 与
与![]() 垂直的直线
垂直的直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为线段
为线段![]() 中点,若
中点,若![]() 的面积
的面积 ![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ,(2)
,(2)![]() .
.
【解析】
(1)根据![]() 的坐标满足圆
的坐标满足圆![]() 方程
方程![]() 可得到
可得到![]() 的值,圆心
的值,圆心![]() 满足
满足![]() ,故圆心
,故圆心![]() 在椭圆上,将其代入可得椭圆方程;
在椭圆上,将其代入可得椭圆方程;
(2)由题意可知,![]() 与直线
与直线![]() 平行,故点
平行,故点![]() 到直线
到直线![]() 的距离即为点
的距离即为点![]() 到直线
到直线![]() 的距离,从而可以用
的距离,从而可以用![]() 表示出点
表示出点![]() 到直线
到直线![]() 的距离,再用
的距离,再用![]() 计算出弦长
计算出弦长![]() ,从而得出关于
,从而得出关于![]() 的方程,进而得出结果.
的方程,进而得出结果.
解:(1)因为![]() 的坐标满足圆
的坐标满足圆![]() 方程
方程![]() ,
,
故当![]() 时,
时,![]() ,
,
即![]() ,故
,故![]() ,
,
因为圆心![]() 满足
满足![]() ,
,
所以点![]() 在椭圆上,
在椭圆上,
故有![]() ,
,
联立方程组 ,解得
,解得 ,
,
所以椭圆方程为![]() ;
;
(2)因为直线![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为线段
为线段![]() 中点,
中点,
所以![]() 与直线
与直线![]() 垂直,
垂直,
又因为直线![]() 与直线
与直线![]() 垂直,
垂直,
所以![]() 与直线
与直线![]() 平行,
平行,
所以点![]() 到直线
到直线![]() 的距离即为点
的距离即为点![]() 到直线
到直线![]() 的距离,
的距离,
即点![]() 到直线
到直线![]() 的距离为
的距离为 ,
,
设点![]()
联立方程组 ,
,
解得![]() ,
,
由韦达定理可得 ,
,
 ,
,
所以 ,
,
所以![]() 的面积为
的面积为 ,
,
所以 ,
,
即 ,
,
两边同时平方,化简得,![]()
解得![]() 或
或![]() (舍)
(舍)
故![]() .
.

【题目】某学校为了解高一新生的体质健康状况,对学生的体质进行了测试. 现从男、女生中各随机抽取![]() 人,把他们的测试数据,按照《国家学生体质健康标准》整理如下表. 规定:数据≥
人,把他们的测试数据,按照《国家学生体质健康标准》整理如下表. 规定:数据≥![]() ,体质健康为合格.
,体质健康为合格.
等级 | 数据范围 | 男生人数 | 男生平均分 | 女生人数 | 女生平均分 |
优秀 |
|
|
|
|
|
良好 |
|
|
|
|
|
及格 |
|
|
|
|
|
不及格 |
|
|
|
|
|
总计 | -- |
|
|
|
|
(I)从样本中随机选取一名学生,求这名学生体质健康合格的概率;
(II)从男生样本和女生样本中各随机选取一人,求恰有一人的体质健康等级是优秀的概率;
(III)表中优秀、良好、及格、不及格四个等级的男生、女生平均分都接近(二者之差的绝对值不大于![]() ),但男生的总平均分却明显高于女生的总平均分.研究发现,若去掉四个等级中一个等级的数据,则男生、女生的总平均分也接近,请写出去掉的这个等级.(只需写出结论)
),但男生的总平均分却明显高于女生的总平均分.研究发现,若去掉四个等级中一个等级的数据,则男生、女生的总平均分也接近,请写出去掉的这个等级.(只需写出结论)
【题目】十八大以来,我国新能源产业迅速发展.以下是近几年某新能源产品的年销售量数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
新能源产品年销售 | 1.6 | 6.2 | 17.7 | 33.1 | 55.6 |
(1)请画出上表中年份代码![]() 与年销量
与年销量![]() 的数据对应的散点图,并根据散点图判断.
的数据对应的散点图,并根据散点图判断.
![]() 与
与![]() 中哪一个更适宜作为年销售量
中哪一个更适宜作为年销售量![]() 关于年份代码
关于年份代码![]() 的回归方程类型;
的回归方程类型;
(2)根据(Ⅰ)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程,并预测2019年某新能源产品的销售量(精确到0.01).
的回归方程,并预测2019年某新能源产品的销售量(精确到0.01).
参考公式: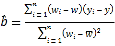 ,
,![]() .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.