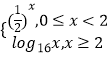Question

【题目】证明．
（1）用数学归纳法证明：12+22+32+…+n2= ，n是正整数；
（2）用数学归纳法证明不等式：1+ + +…+ ＜2 （n∈N*）

Answer 1

【答案】
（1）证明：①n=1时，左边=12=1，右边= =1，等式成立，

②假设n=k时，等式成立，即12+22+32+…+k2= ，

则n=k+1时，12+22+32+…+k2+（k+1）2= +（k+1）2

= [2k2+k+6（k+1）]

= （2k2+7k+6）

= = ．

∴当n=k+1时，等式成立，

由①②得：12+22+32+…+n2= ．

（2）证明：①n=1时，显然不等式成立，

②假设n=k时，不等式成立，即1+ + +…+ ＜2 ．

则当n=k+1时，1+ + +…+ + ＜2 + = ＜ =2 ．

∴当n=k+1时，不等式成立．

由①②得1+ + +…+ ＜2 ．

【解析】根据数学归纳法的证明步骤先验证n=1时结论成立，再假设n=k时，结论成立，推导n=k+1时结论成立即可．
【考点精析】认真审题，首先需要了解数学归纳法的定义(数学归纳法是证明关于正整数n的命题的一种方法)．