题目内容
某商品每件成本9元,售价为30元,每星期卖出144件. 如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值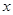 (单位:元,
(单位:元, )的平方成正比.
)的平方成正比.
已知商品单价降低2元时,一星期多卖出8件.
(1)将一个星期的商品销售利润表示成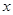 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
(1)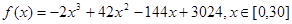 (2)见解析
(2)见解析
解析试题分析:(1)先设商品降价x元,写出多卖的商品数,则可计算出商品在一个星期的获利数,再依题意:“商品单价降低2元时,一星期多卖出24件”求出比例系数即可得一个星期的商品销售利润表示成x的函数;
(2)根据(1)中得到的函数,利用导数研究其极值,从而救是f(x)达到极大值.从而得出所以定价为多少元时,能使一个星期的商品销售利润最大.
试题解析:解:(1)设商品降价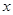 元,则每个星期多卖的商品数为
元,则每个星期多卖的商品数为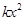 ,若记商品在一个星期的获利为
,若记商品在一个星期的获利为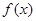 ,则依题意有
,则依题意有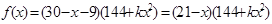 , 3分
, 3分
又由已知条件,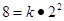 ,于是有
,于是有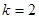 , 5分
, 5分
所以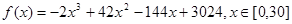 6分
6分
(2)由(1)得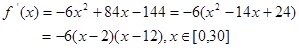 7分
7分
当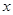 变化时,
变化时,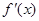 与
与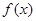 的变化如下表:
的变化如下表:
10分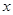
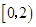
2 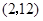
12 
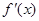
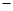
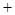
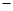
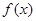
↘ 极小 ↗ 极大 ↘
故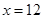 时,
时,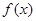 达到极大值.因为
达到极大值.因为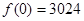 ,
,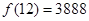 ,
,
所以定价为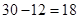 元能使一个星期的商品销售利润最大. 13分
元能使一个星期的商品销售利润最大. 13分
考点:函数模型的选择与应用.

练习册系列答案
相关题目
 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
. 时,求直路
时,求直路
 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度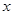 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当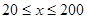 时,车流速度
时,车流速度 时,求函数
时,求函数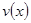 的表达式;
的表达式;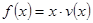 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)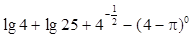 .
. (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: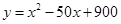 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为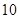 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;
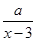 +10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
+10(x-6)2,其中3<x<6,a为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.