题目内容
在△ABC中,角A、B、C的对边分别为a、b、c,且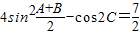 .
.(1)求角C的大小;
(2)若a+b=5,c=
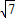 ,求△ABC的面积.
,求△ABC的面积.
【答案】分析:(1)在△ABC中,利用诱导公式与降幂公式可求得cosC= ,从而可求得角C的大小;
,从而可求得角C的大小;
(2)利用余弦定理可求得(a+b)2-3ab=7,再结合已知条件a+b=5即可求得ab,从而可求S△ABC.
解答:解:(1)∵A+B+C=180°
由4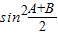 -cos2C=
-cos2C= 得4
得4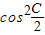 -cos2C=
-cos2C= …(1分)
…(1分)
∴4•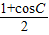 -(2cos2C-1)=
-(2cos2C-1)= …(3分)
…(3分)
整理,得4cos2C-4cosC+1=0…(4分)
解得:cosC= …(5分)
…(5分)
∵0°<C<180°,
∴C=60°…(6分)
(2)解:由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-ab …(7分)
∴7=(a+b)2-3ab…(8分)
由条件a+b=5得 7=25-3ab,ab=6 …(10分)
∴S△ABC= absinC=
absinC= ×6×
×6×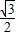 =
=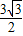 …(12分)
…(12分)
点评:本题考查诱导公式与降幂公式,考查余弦定理与三角形的面积公式,考查转化思想与运算能力,属于中档题.
 ,从而可求得角C的大小;
,从而可求得角C的大小;(2)利用余弦定理可求得(a+b)2-3ab=7,再结合已知条件a+b=5即可求得ab,从而可求S△ABC.
解答:解:(1)∵A+B+C=180°
由4
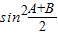 -cos2C=
-cos2C= 得4
得4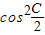 -cos2C=
-cos2C= …(1分)
…(1分)∴4•
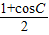 -(2cos2C-1)=
-(2cos2C-1)= …(3分)
…(3分)整理,得4cos2C-4cosC+1=0…(4分)
解得:cosC=
 …(5分)
…(5分)∵0°<C<180°,
∴C=60°…(6分)
(2)解:由余弦定理得:c2=a2+b2-2abcosC,即7=a2+b2-ab …(7分)
∴7=(a+b)2-3ab…(8分)
由条件a+b=5得 7=25-3ab,ab=6 …(10分)
∴S△ABC=
 absinC=
absinC= ×6×
×6×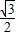 =
=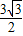 …(12分)
…(12分)点评:本题考查诱导公式与降幂公式,考查余弦定理与三角形的面积公式,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |