Question

已知函数f（x）=（x²+ax+2）e^x，（x，a∈R）．
（Ⅰ）若f（x）在R上单调，求a的取值范围；
（Ⅱ）当a=-

5

2

时，求函数f（x）的极小值．

Answer 1

分析：（I）先求出函数的导数，f（x）在R上单调等价于x²+（a+2）x+a+2≥0恒成立，下面只要二次函数的根的判别式△≤0即可求得a的取值范围；
（Ⅱ）利用导数研究函数的极小值．先求出在函数的导数，再结合导数值为0求出极值点，最后结合函数的单调性即可求得函数f（x）的极小值．

解答：解：f′（x）=e^x[x²+（a+2）x+a+2]
（Ⅰ）f′（x）=e^x[x²+（a+2）x+a+2]，
考虑到e^x＞0恒成立且x²系数为正，
∴f（x）在R上单调等价于x²+（a+2）x+a+2≥0恒成立．
∴（a+2）²-4（a+2）≤0，
∴-2≤a≤2，即a的取值范围是[-2，2]，（8分）
（若得a的取值范围是（-2，2），可扣1分）
（Ⅱ）当a=-

5

2

时，f(x)=(x2-

5

2

x+2)ex，f′(x)=ex(x2-

1

2

x-

1

2

)，（10分）
令f′（x）=0，得x=-

1

2

，或x=1??，
令f′（x）＞0，得x＜-

1

2

，或x＞1??，
令f′（x）＜0，得-

1

2

＜x＜1??（12分）
x，f′（x），f（x）的变化情况如下表
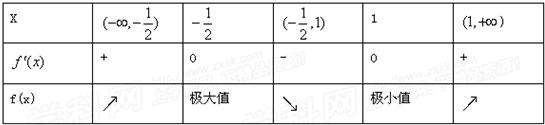
所以，函数f（x）的极小值为f（1）=

1

2

e（14分）

点评：本小题主要考查利用导数研究函数的单调性、利用导数研究函数的极值等基础知识，考查运算求解能力．属于基础题．