题目内容
如图所示,四棱锥P—ABCD,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.(1)求证:MN∥平面PAD;
(2)若MN⊥平面PCD,求二面角P-CD-A的大小.
解:(方法一)
(1)过N作NE∥CD交PD于E,连接AE
∴N为PC中点 ∴EN![]()
![]() CD
CD
又∵AB![]() CD ∴EN
CD ∴EN![]()
![]() AB
AB
又∵M为AB的中点 ∴EN![]() AM
AM
∴四边形ENMA为平行四边形
∴MN∥平面PAD(6分)
(2)∵PA⊥平面ABCD 又∵底面为矩形
∴PD⊥CD ∴∠PDA即为二面角P-CD-A的平面角
又∵AE∥MN,MN⊥平面PCD ∴AE⊥平面PCD
∴AE⊥PD 又∵E为PD中点
∴△PAD为等腰直角三角形
∴∠PDA=45°
∴二面角P-CD-A的大小为45°
(方法二)如图建立空间直角坐标系
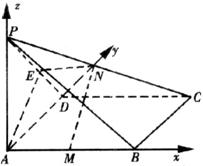
设AB=a,AD=b,PA=c
则A(0,0,0),B(a,0,0),C(a,b,0),P(0,0,c),
D(0,b,0),M(![]() ,0,0),N(
,0,0),N(![]() )
)
(1)∵![]() (0,b,0)+
(0,b,0)+![]() (0,0,c)=
(0,0,c)=![]() ,
,
∴![]() ∥平面PAD
∥平面PAD
(2)∵MN⊥平面PCD PA⊥平面ABCD
∴![]() 是平面PCD的法向量,
是平面PCD的法向量,![]() 是平面ABCD的法向量
是平面ABCD的法向量
又由![]() =(0,-b,c)得
=(0,-b,c)得
![]() ·(0,-b,0)=0
·(0,-b,0)=0
∴b=c
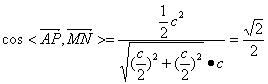
∴二面角P-DC-A的大小为45°

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3,PC=CD=2,PC⊥底面ABCD,E为AB的中点.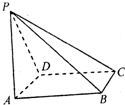 如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,
如图所示,四棱锥P-ABCD的底面是一个矩形,AB=3.AD=1.又PA⊥AB,PA=4,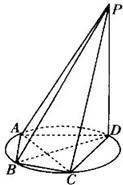 如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD.
如图所示,四棱锥P-ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP~△BAD. (2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点.
(2012•烟台一模)如图所示,四棱锥P-ABCD中,ABCD为正方形,PA⊥AD,E,F,G分别是线段PA,PD,CD的中点. 如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD底面是直角梯形,BA⊥AD,CD⊥AD,CD=2AB,PA⊥底面ABCD,E为PC的中点,PA=AD=AB=1.