Question

（本题满分15分）

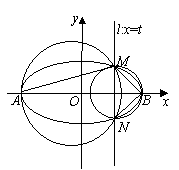已知椭圆的离心率为，椭圆的左、右两个顶点分别为A，B，AB=4，直线与椭圆相交于M，N两点，经过三点A，M，N的圆与经过三点B，M，N的圆分别记为圆C1与圆C2．

（1）求椭圆的方程；

（2）求证：无论t如何变化，圆C1与圆C2的圆心距是定值；

（3）当t变化时，求圆C1与圆C2的面积的和S的最小值．

Answer 1

解：（1）由题意：可得：，

故所求椭圆方程为：1           ………………………3分

（2）易得A的坐标(－2，0)，B的坐标(2,0)，M的坐标，N的坐标，

线段AM的中点P，

直线AM的斜率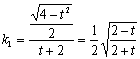 ………………………………………5分

又, 直线的斜率

直线的方程，

的坐标为   同理的坐标为………………………… 8分  

,即无论t如何变化，为圆C1与圆C2的圆心距是定值.…………… 11分

（2）圆的半径为，圆的半径为，

则 （＜＜）

显然时，最小，.                          …………… 15分