题目内容
直线y=kx+1与双曲线x2-y2=1有且仅有一个公共点，则k的取值为（ ）
分析：若直线y=kx+1与双曲线x2-y2=1有且仅有一个公共点，有两种情况：一种是相交，这时直线与双曲线的渐近线平行，另一种是相切，两种情况可以将直线与双曲线联立后一起解决
解答：解：把直线y=kx+1代入双曲线x2-y2=1中，消y，得（1-k2）x2-2kx-2=0
当1-k2=0，即k=±1时，直线与双曲线相交有一个交点
当1-k2≠0，△=0，即4k2+8（1-k2）=0，k=±
时，直线与双曲线相切，有一个交点
∴k的值为±1，±
故选B
当1-k2=0，即k=±1时，直线与双曲线相交有一个交点
当1-k2≠0，△=0，即4k2+8（1-k2）=0，k=±
| 2 |
∴k的值为±1，±
| 2 |
故选B
点评：本题考查了直线与双曲线的位置关系，解题时要分辨清楚直线与双曲线只有一个交点时，不一定是相切，还可能相交，不然就会丢解
练习册系列答案
相关题目
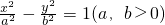的虚轴长为2
，渐近线方程是y=
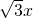，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且
．
的虚轴长为2
，渐近线方程是y=
，O为坐标原点，直线y=kx+m（k，m∈R）与双曲线C相交于A、B两点，且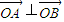
．