题目内容
已知| 2sin2α+sin2α |
| 1+tanα |
| π |
| 4 |
| π |
| 2 |
分析:首先利用二倍角公式和切化弦知识将已知等式转化为单角α的正弦和余弦的等式,再与要求的结果比较,只要平方即可求出.在求解时注意角的范围,三角函数的符号.
解答:解:因为
=2sinαcosα
所以k=2sinαcosα
因而(sinα-cosα)2=1-2sinαcosα=1-k
又
<α<
,于是sinα-cosα>0
因此sinα-cosα=
| 2sin2α+sin2α |
| 1+tanα |
所以k=2sinαcosα
因而(sinα-cosα)2=1-2sinαcosα=1-k
又
| π |
| 4 |
| π |
| 2 |
因此sinα-cosα=
| 1-k |
点评:本题考查利用二倍角公式和切化弦进行三角变换,同时考查sinα-cosα、sinα+cosα、sinα•cosα三者的联系.

练习册系列答案
相关题目
 )+2sin2
)+2sin2 .
. ,△ABC的面积S=
,△ABC的面积S= ,a=
,a= ,求sinB+sinC的值.
,求sinB+sinC的值.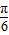 )+2sin2
)+2sin2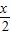 .
. ,△ABC的面积S=
,△ABC的面积S=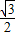 ,a=
,a=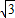 ,求sinB+sinC的值.
,求sinB+sinC的值.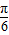 )+2sin2
)+2sin2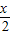 .
. ,△ABC的面积S=
,△ABC的面积S=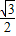 ,a=
,a=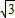 ,求sinB+sinC的值.
,求sinB+sinC的值.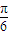 )+2sin2
)+2sin2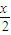 .
. ,△ABC的面积S=
,△ABC的面积S=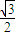 ,a=
,a=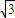 ,求sinB+sinC的值.
,求sinB+sinC的值.