题目内容
当![]() 为正整数时,区间
为正整数时,区间![]() ,
,![]() 表示函数
表示函数![]() 在
在![]() 上函数值取整数值的个数,当
上函数值取整数值的个数,当![]() 时,记
时,记![]() .当
.当![]() ,
,![]() 表示把
表示把![]() “四舍五入”到个位的近似值,如
“四舍五入”到个位的近似值,如![]()
![]() 当
当![]() 为正整数时,
为正整数时,![]() 表示满足
表示满足![]() 的正整数
的正整数![]() 的个数.
的个数.
(1)判断![]() 在区间
在区间![]() 的单调性;
的单调性;
(2)求![]() ;
;
(3)当![]() 为正整数时,集合
为正整数时,集合![]() 中所有元素之和为
中所有元素之和为![]() ,记
,记![]() 求证:
求证:![]()
(1)当![]()
![]()
![]() 为增函数(2)
为增函数(2)![]()
![]()
![]()
![]() (3)见解析
(3)见解析
解析:
(1)∵![]()
∴当![]()
![]()
![]() 为增函数.----------------------2分
为增函数.----------------------2分
(2)由(1) ![]() 在
在![]() 为增函数,又
为增函数,又![]()
∴![]() --------------------------------------------------3分
--------------------------------------------------3分
同理![]() 时,
时,![]()
![]() 为增函数,
为增函数,
![]() ∴
∴![]() -----------------------4分
-----------------------4分
∴![]() -----------------------------------------5分
-----------------------------------------5分
又∵![]() 表示满足
表示满足![]() 的正整数
的正整数![]() 的个数.
的个数.
∴![]()
∴![]()
![]()
∴![]() -----------------------------------------------6分
-----------------------------------------------6分
(3)又∵![]() 表示满足
表示满足![]() 的正整数
的正整数![]() 的个数,
的个数,
∴![]() --------------------------------8分
--------------------------------8分
∴![]()
∴![]() 共
共![]() 个.
个.
∴![]() ------------------------------------------10分
------------------------------------------10分
![]()
![]()
∴![]()
![]()
![]()
![]()
![]()
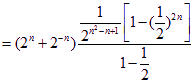 =
=![]()
![]() ----------------------------------------12分
----------------------------------------12分
∴![]()
![]()
![]()
![]() ----------------14分
----------------14分

练习册系列答案
相关题目
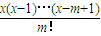 ,其中x∈R,m是正整数,且Cx=1,这是组合数Cmn(n、m是正整数,且m≤n)的一种推广.
,其中x∈R,m是正整数,且Cx=1,这是组合数Cmn(n、m是正整数,且m≤n)的一种推广.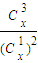 取得最小值?
取得最小值?