题目内容
(1)设全集为R,集合A={x|3≤x<7},集合B={x|2<x<8},求(?RA)∩B.
(2)0.064-
-(-
)0+16
+0.25
+2log36-log312.
(2)0.064-
| 1 |
| 3 |
| 1 |
| 8 |
| 3 |
| 4 |
| 1 |
| 2 |
分析:(1)根据集合的基本运算进行计算即可.
(2)根据指数幂和对数的运算法则进行计算即可.
(2)根据指数幂和对数的运算法则进行计算即可.
解答:解:(1)∵A={x|3≤x<7},
∴CRA={x|x<3,或x≥7},
故 (CRA)∩B={x|2<x<3,或7≤x<8}.
(2)原式=[(0.4)3]-
-1+(24)
+0.5+log336-log312=(0.4)-1-1+8+0.5+log33=2.5-1+8+0.5+1=11.
∴CRA={x|x<3,或x≥7},
故 (CRA)∩B={x|2<x<3,或7≤x<8}.
(2)原式=[(0.4)3]-
| 1 |
| 3 |
| 3 |
| 4 |
点评:本题主要考查集合的基本运算以及指数幂和对数的计算,比较计算.

练习册系列答案
相关题目
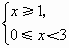 的解集为A,则
的解集为A,则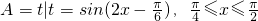 ,若不等式t2+at+b≤0的解集是A,求a,b的值.
,若不等式t2+at+b≤0的解集是A,求a,b的值.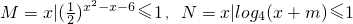 ,若M∩N=Φ,求实数m的取值范围.
,若M∩N=Φ,求实数m的取值范围.