Question

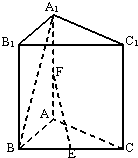直三棱柱ABC-A₁B₁C₁的底面为等腰直角三角形，∠BAC=90°，AB=AC=2，AA₁=2

2

，E、F分别是BC、AA₁的中点．求：
（Ⅰ）FE与底面所成角的大小；
（Ⅱ）异面直线EF和A₁B所成角的大小．

Answer 1

分析：（Ⅰ）由已知可得FA⊥平面ABC，可得∠FEA即为FE与底面所成角，由等腰直角三角形，∠BAC=90°，AB=AC=2，E为BC的中点 可求AE，在Rt△AEF中求解即可
（Ⅱ）由E，F都为中点，考虑取AB的中点G，则可得FG∥BA₁，从而有∠GFE即为异面直线EF和A₁B所成角（或补角）分别求解FE，EG，FG，从而可求

解答：解：（Ⅰ）连接FE，由已知可得FA⊥平面ABC
∴∠FEA即为FE与底面所成角
∵等腰直角三角形，∠BAC=90°，AB=AC=2，E为BC的中点∴AE=

2

∵△AEF中AF=

2

，AE=

2

∴∠AEF=45°即FE与底面所成角45°
（Ⅱ）取AB的中点G，连接FG，EG则可得FG∥BA₁
所以∠GFE即为异面直线EF和A₁B所成角（或补角）
由（Ⅰ）可得FE=2，为FG=

1

2

BA1=

3

，EG=1
所以可得∠GFE=30°
异面直线EF和A₁B所成角的大小为30°

点评：本题所考查的时立体几何中最为基本的类型的试题：直线与平面所成的角的求解与异面直线所成的角度的求解，解决此问题的关键是要能够做出所要求的角，然后再通过解三角形进行求解．