题目内容
已知向量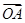 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3),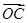 =(5-m,-3-m).
=(5-m,-3-m).
(1)若点A,B,C不能构成三角形,求实数m满足的条件;
若△ABC为直角三角形,求实数m的值.
(1)m=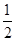 ;(2)m=
;(2)m=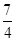 或-
或-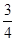 或
或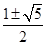 .
.
解析试题分析:(1)利用向量的运算法则求出 ,
, ;利用向量垂直的充要条件列出方程求出m.
;利用向量垂直的充要条件列出方程求出m.
(2)将构成三角形转化为三点不共线,,将几何中的角为直角转化为向量的语言,通过向量的数量积为零列出关于实数m的方程,求解出实数m.
(1)∵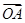 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3),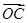 =(5-m,-3-m),若A,B,C三点不能构成三角形,则这三点共线,∵
=(5-m,-3-m),若A,B,C三点不能构成三角形,则这三点共线,∵ =(3,1),
=(3,1), =(2-m,1-m),∴3(1-m)=2-m,∴m=
=(2-m,1-m),∴3(1-m)=2-m,∴m=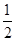 即为满足的条件.(2)由题意,△ABC为直角三角形,①若∠A=90°,则
即为满足的条件.(2)由题意,△ABC为直角三角形,①若∠A=90°,则 ⊥
⊥ ,∴3(2-m)+(1-m)=0,∴m=
,∴3(2-m)+(1-m)=0,∴m=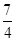 .②若∠B=90°,则
.②若∠B=90°,则 ⊥
⊥ ,∵
,∵ (-1-m,-m),∴3(-1-m)+(-m)=0,∴m=-
(-1-m,-m),∴3(-1-m)+(-m)=0,∴m=-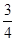 . ③若∠C=90°,则
. ③若∠C=90°,则 ⊥
⊥ , ∴(2-m)(-1-m)+(1-m)(-m)=0,∴m=
, ∴(2-m)(-1-m)+(1-m)(-m)=0,∴m=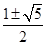 .综上可得,m=
.综上可得,m=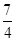 或-
或-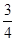 或
或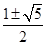 .
.
考点:平面向量共线(平行)的坐标表示;数量积判断两个平面向量的垂直关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列 的通项公式为
的通项公式为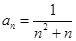 ,其前
,其前 项和为
项和为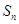 ,则
,则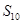 的值为 ( )
的值为 ( )
A.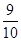 | B.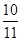 | C.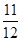 | D.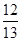 |
 满足
满足 ,则函数
,则函数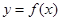 的表达式为 .
的表达式为 .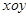 平面上,点
平面上,点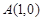 ,点
,点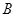 在单位圆上,
在单位圆上,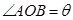 (
(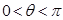 )
)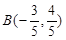 ,求
,求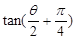 的值;
的值;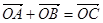 ,四边形
,四边形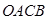 的面积用
的面积用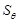 表示,求
表示,求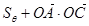 的取值范围.
的取值范围.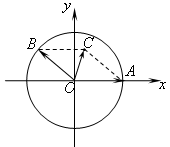
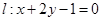 与⊙C:
与⊙C: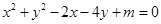 (
(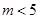 )
)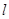 与⊙C相交,求
与⊙C相交,求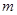 的取值范围。
的取值范围。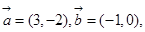
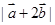 ;
;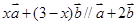 时,求
时,求 的值.
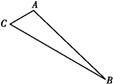
的值.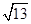 ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足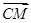 =λ
=λ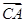 +μ
+μ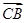 ,且λμ=
,且λμ= .
.
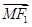 |-|
|-|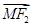 ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.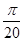 ,求证:a∥b.
,求证:a∥b. =-2i+mj,
=-2i+mj, =ni+j,
=ni+j,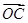 =5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.
=5i-j,若点A、B、C在同一条直线上,且m=2n,求实数m、n的值.