题目内容
设函数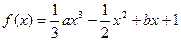 在点A(1,f(1))处的切线平行于x轴.
在点A(1,f(1))处的切线平行于x轴.
(Ⅰ)当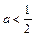 时,讨论函数
时,讨论函数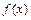 的单调性;
的单调性;
(Ⅱ)证明:当a=-3时,对任意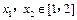 ,都有
,都有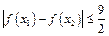
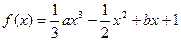 在点A(1,f(1))处的切线平行于x轴.
在点A(1,f(1))处的切线平行于x轴.(Ⅰ)当
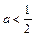 时,讨论函数
时,讨论函数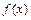 的单调性;
的单调性;(Ⅱ)证明:当a=-3时,对任意
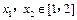 ,都有
,都有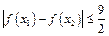
解:(Ⅰ)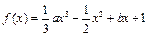 ,
,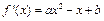 ,
,
∴ ,∴
,∴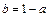 ……………………………………1分
……………………………………1分
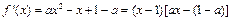 .
.
(1)当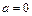 时,
时,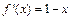 ,
,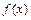 的递增区间为
的递增区间为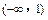 ,
,
递减区间为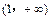 ; ………………………2分
; ………………………2分
(2)当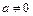 时,
时,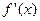 =0的两个根为x1=1和x2=
=0的两个根为x1=1和x2=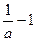 ,
,
若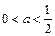 ,则
,则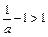 ,
,
由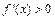 得
得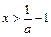 或
或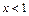 ,由
,由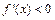 得
得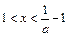 ;
;
∴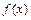 的递增区间为
的递增区间为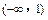 和
和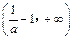 ,
,
递减区间为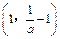 . …………………4分
. …………………4分
若 ,则
,则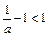 ,
,
由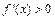 得
得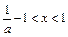 ,由
,由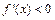 得
得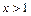 或
或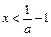 ,
,
 ∴
∴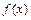 的递增区间为
的递增区间为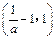 ,
,
递减区间为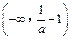 和
和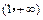 . ……………………6分
. ……………………6分
 (Ⅱ)当
(Ⅱ)当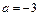 时,
时,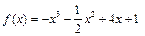
由(Ⅰ)知,函数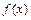 在
在 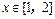 为减函数,
为减函数,
∴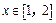 ,
,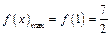 ,
,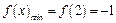 ,
,
∴对任意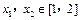 ,
,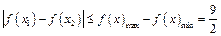 ,
,
即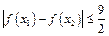 . ……………………………………………12分
. ……………………………………………12分
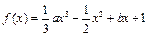 ,
,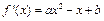 ,
,∴
 ,∴
,∴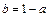 ……………………………………1分
……………………………………1分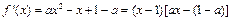 .
.(1)当
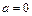 时,
时,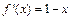 ,
,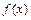 的递增区间为
的递增区间为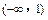 ,
,递减区间为
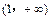 ; ………………………2分
; ………………………2分(2)当
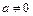 时,
时,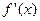 =0的两个根为x1=1和x2=
=0的两个根为x1=1和x2=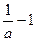 ,
,若
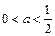 ,则
,则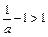 ,
,由
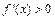 得
得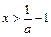 或
或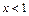 ,由
,由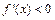 得
得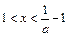 ;
;∴
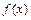 的递增区间为
的递增区间为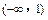 和
和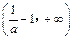 ,
,递减区间为
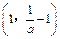 . …………………4分
. …………………4分若
 ,则
,则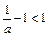 ,
,由
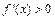 得
得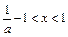 ,由
,由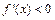 得
得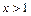 或
或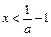 ,
, ∴
∴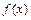 的递增区间为
的递增区间为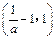 ,
,递减区间为
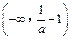 和
和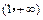 . ……………………6分
. ……………………6分 (Ⅱ)当
(Ⅱ)当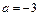 时,
时,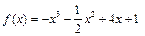
由(Ⅰ)知,函数
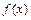 在
在 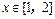 为减函数,
为减函数,∴
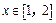 ,
,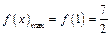 ,
,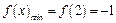 ,
,∴对任意
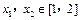 ,
,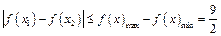 ,
,即
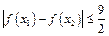 . ……………………………………………12分
. ……………………………………………12分略

练习册系列答案
相关题目
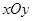 中,已知点P是函数
中,已知点P是函数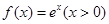 的图象上的动点,该图象在P处的切线
的图象上的动点,该图象在P处的切线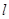 交y轴于点M,过点P作
交y轴于点M,过点P作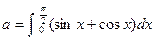 ,则二项式
,则二项式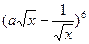 的展开式中含
的展开式中含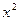 项的系数是
项的系数是 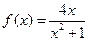 在区间
在区间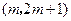 上是单调递增函数,则实数
上是单调递增函数,则实数 的取值范围是
的取值范围是 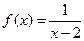 的反函数为
的反函数为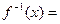 。
。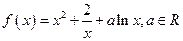
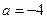 ,求函数
,求函数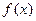 的单调区间;
的单调区间;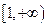 上单调递增,求实数
上单调递增,求实数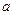 的取值范围
的取值范围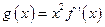 ,若
,若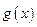 的最小值是
的最小值是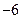 ,求函数
,求函数 ,
,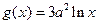 ,其中
,其中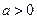 .若两曲线
.若两曲线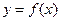 ,
,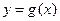 有公共点,且在该点处的切线相同.则
有公共点,且在该点处的切线相同.则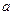 的值为 . (定义:
的值为 . (定义: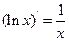 ).
).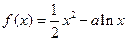 的图象在点
的图象在点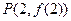 处的切线方程为
处的切线方程为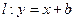
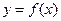 的表达式和切线
的表达式和切线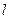 的方程;
的方程;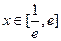 时(其中
时(其中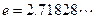 ),不等式
),不等式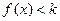 恒成立,求实数
恒成立,求实数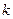 的取值范围.
的取值范围.
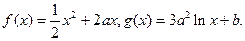
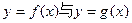 有公共点,且在公共点处的切线相同,若
有公共点,且在公共点处的切线相同,若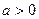 ,试建立
,试建立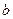 关于
关于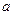 的函数关系式,并求
的函数关系式,并求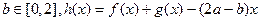 在(0,4)上为单调函数,求
在(0,4)上为单调函数,求