题目内容
已知各项均不相等的等差数列{an}的前四项和为10, 是一个与n无关的常数,数列{an}的前n项和为Sn.
是一个与n无关的常数,数列{an}的前n项和为Sn.
(1)求数列{an}的通项公式及数列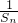 的前n项和Tn;
的前n项和Tn;
(2)若a1,a2,a4恰为等比数列{bn}的前三项,记数列cn=an(cosnπ+bn),求{cn}的前n项和为Kn.
解(1)∵ 是一个与n无关的常数,∴a1=d.
是一个与n无关的常数,∴a1=d.
又 ,∴a1=1,
,∴a1=1,
∴an=n,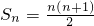 ,
,
∴ ,
,
∴Tn= …+
…+ =
= …+
…+ =
= =
= .
.
(2)∵b1=a1=1,b2=a2=2, 是等比数列{bn}的前3项,
是等比数列{bn}的前3项,
∴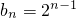 .
.
∴cn=n(-1)n+n×2n-1,
记 ,
,
则 ,
,
Bn=1+2×21+3×22+…n×2n-1=(n-1)2n+1.
Kn= .
.
分析:(1)利用等差数列的通项公式和前n项和公式及裂项求和即可求出;
(2)利用等比数列的前n项和公式即可求出.注意对n分奇偶讨论.
点评:熟练掌握等差数列和等比数列的通项公式和前n项和公式是解题的关键.
 是一个与n无关的常数,∴a1=d.
是一个与n无关的常数,∴a1=d.又
 ,∴a1=1,
,∴a1=1,∴an=n,
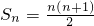 ,
,∴
 ,
,∴Tn=
 …+
…+ =
= …+
…+ =
= =
= .
.(2)∵b1=a1=1,b2=a2=2,
 是等比数列{bn}的前3项,
是等比数列{bn}的前3项,∴
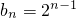 .
.∴cn=n(-1)n+n×2n-1,
记
 ,
,则
 ,
,Bn=1+2×21+3×22+…n×2n-1=(n-1)2n+1.
Kn=
 .
.分析:(1)利用等差数列的通项公式和前n项和公式及裂项求和即可求出;
(2)利用等比数列的前n项和公式即可求出.注意对n分奇偶讨论.
点评:熟练掌握等差数列和等比数列的通项公式和前n项和公式是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 的前四项和
的前四项和 ,且
,且 成等比.
成等比. 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值. 的前四项和
的前四项和 ,且
,且 成等比.
成等比. 为数列
为数列 的前n项和,若
的前n项和,若 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.