题目内容

已知圆O：x2+y2=1和抛物线y=x2-2上三个不同的点P、Q、R.如果直线PQ和PR都与圆O相切.求证：直线QR也与圆O相切.

证明：设P（a,a2-2）,Q(b,b2-2),R(c,c2-2),则直线PQ、PR、QR的方程分别为

（a+b）x-y-ab-2=0、(a+c)x-y-ac-2=0、(b+c)x-y-bc-2=0.

由于PQ是圆O的切线，则

=1，即（a2-1）b2+2ab+3-a2=0.

同理：（a2-1）c2+2ac+3-a2=0,

∴b、c是方程(a2-1)x2+2ax+3-a2=0的两根.则有b+c=,bc=.

故圆心O到直线QR的距离

d=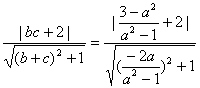=1,

即直线QR与圆O相切.

练习册系列答案
相关题目
精英家教网已知圆O：x2+y2=2交x轴于A，B两点，曲线C是以AB为长轴，离心率为
2
2
的椭圆，其左焦点为F．若P是圆O上一点，连接PF，过原点O作直线PF的垂线交椭圆C的左准线于点Q．
（1）求椭圆C的标准方程；
（2）若点P的坐标为（1，1），求证：直线PQ与圆O相切；
（3）试探究：当点P在圆O上运动时（不与A、B重合），直线PQ与圆O是否保持相切的位置关系？若是，请证明；若不是，请说明理由．
精英家教网已知圆o：x2+y2=b2与椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)有一个公共点A（0，1），F为椭圆的左焦点，直线AF被圆所截得的弦长为1．
（1）求椭圆方程．
（2）圆o与x轴的两个交点为C、D，B（ x0，y0）是椭圆上异于点A的一个动点，在线段CD上是否存在点T（t，0），使|BT|=|AT|，若存在，请说明理由．
已知圆O：x2+y2=9，定点 A（6，0），直线l：3x-4y-25=0
（1）若P为圆O上动点，求线段PA的中点M的轨迹方程
（2）设E、F分别是圆O和直线l上任意一点，求线段EF的最小值．
（2012•广州一模）已知圆O：x2+y2=r2，点P（a，b）（ab≠0）是圆O内一点，过点P的圆O的最短弦所在的直线为l1，直线l2的方程为ax+by+r2=0，那么（　　）
已知圆O：x2+y2=1，点P在直线x=
3
上，O为坐标原点，若圆O上存在点Q，使∠OPQ=30°，则点P的纵坐标y0的取值范围是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网