题目内容
下列命题正确的是( )A.已知p:
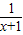 >0,则-p:
>0,则-p: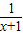 ≤0
≤0B.存在实数x∈R,使sinx+cosx=
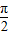 成立
成立C.命题p:对任意的x∈R,x2+x+1>0,则-p:对任意的x∈R,x2+x+1≤0
D.若p或q为假命题,则p,q均为假命题
【答案】分析:由于原命题中X=-1时,不等式无意义,故否定中应包含x=-1,进而判断A的真假;
根据三角函数的值域,分析出sinx+cosx的取值范围,进而判断B的真假;
根据全称命题的否定一定是一个特称命题,可判断C的真假;
根据复合命题真假判断的真值表,可以判断D的真假.
解答:解:已知p: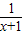 >0,则-p:
>0,则-p: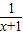 ≤0或x=-1,故A错误;
≤0或x=-1,故A错误;
sinx+cosx∈[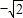 ,
,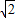 ],故存在实数x∈R,使sinx+cosx=
],故存在实数x∈R,使sinx+cosx=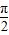 成立错误;
成立错误;
命题p:对任意的x∈R,x2+x+1>0,则-p:存在x∈R,x2+x+1≤0,故C错误;
根据p或q一真为真,同假为假的原则,可得若p或q为假命题,则p,q均为假命题,故D正确
故选D
点评:本题考查的知识点是命题的真假判断,熟练掌握命题的否定,三角函数的值域,复合命题真假判断真值表等基本知识点是解答的关键.
根据三角函数的值域,分析出sinx+cosx的取值范围,进而判断B的真假;
根据全称命题的否定一定是一个特称命题,可判断C的真假;
根据复合命题真假判断的真值表,可以判断D的真假.
解答:解:已知p:
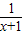 >0,则-p:
>0,则-p: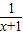 ≤0或x=-1,故A错误;
≤0或x=-1,故A错误;sinx+cosx∈[
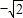 ,
,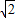 ],故存在实数x∈R,使sinx+cosx=
],故存在实数x∈R,使sinx+cosx=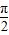 成立错误;
成立错误;命题p:对任意的x∈R,x2+x+1>0,则-p:存在x∈R,x2+x+1≤0,故C错误;
根据p或q一真为真,同假为假的原则,可得若p或q为假命题,则p,q均为假命题,故D正确
故选D
点评:本题考查的知识点是命题的真假判断,熟练掌握命题的否定,三角函数的值域,复合命题真假判断真值表等基本知识点是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目