题目内容

方程为x²+y²+4x=x-y+1的曲线上任意两点之间距离的最大值为________．

$\text{[math]}$
分析：先化简所给的方程为 $\text{[math]}$ ，利用圆上任意两点间的距离最大值为圆的直径．
解答：方程 x²+y²+4x=x-y+1 即 $\text{[math]}$ ，
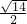表示以（- $\text{[math]}$ ，- $\text{[math]}$ ）为圆心，以 $\text{[math]}$ 为半径的圆，
故x²+y²+4x=x-y+1的曲线上任意两点之间距离的最大值为圆的直径 $\text{[math]}$ ，
故答案为 $\text{[math]}$ ．
点评：本题考查圆的标准方程，利用圆上任意两点间的距离最大值为圆的直径．

练习册系列答案

初中单元练习与测试系列答案

优质课堂快乐成长系列答案

智慧大考卷系列答案

导学案广东经济出版社系列答案

优佳好书系讲与练系列答案

课课练与单元检测系列答案

高中基础训练山东教育出版社系列答案

名校学案名校小状元系列答案

全优课堂满分备考系列答案

专题王系列答案

相关题目

如图，圆O的方程为x²+y²=4，
（1）已知点A的坐标为（2，0），B为圆周上任意一点，求弧

长小于π的概率；
（2）若P（x，y）为圆O内任意一点，求P到原点的距离大于1的概率．

（2013•许昌三模）已知圆C的方程为x²+y²=4，过点M（2，4）作圆C的两条切线，切点分别为A，B，直线AB恰好经过椭圆T：

=1(a＞b＞0)的右顶点和上顶点．
（1）求椭圆T的方程；
（2）已知直线l与椭圆T相交于P，Q两不同点，直线l方程为y=kx+

(k＞0)，O为坐标原点，求△OPQ面积的最大值．

已知圆的方程为x²+y²=4，过点M（2，4）作圆的两条切线，切点分别为A₁、A₂，直线A₁A₂恰好经过椭圆

=1(a＞b＞0)的右顶点和上顶点．
（Ⅰ）求椭圆的方程；
（Ⅱ）设AB是椭圆

=1（a＞b＞0）垂直于x轴的一条弦，AB所在直线的方程为x=m（|m|＜a且m≠0），P是椭圆上异于A、B的任意一点，直线AP、BP分别交定直线l：x=

于两点Q、R，求证

已知圆C的方程为x²+y²=4，动点P满足：过点P作直线与圆C相交所得的所有弦中，弦长最小的为2，记所有满足条件的点P形成的几何图形为曲线M．
（1）写出曲线M所对应的方程；（不需要解答过程）
（2）过点S（0，2）的直线l与圆C交于A，B两点，与曲线M交于E，F两点，若AB=2EF，求直线l的方程；
（3）设点T（x₀，y₀）．
①当y₀=0时，若过点T存在一对互相垂直的直线同时与圆C有两个公共点，求实数x₀的取值范围；
②若过点T存在一对互相垂直的直线同时与圆C有两个公共点，试探求实数x₀，y₀应满足的条件．

已知圆C的方程为x²+y²=4，过点M（2，4）作圆C的两条切线，切点分别为A，B，直线AB恰好经过椭圆T：

(a＞b＞0)的右顶点和上顶点．
（1）求椭圆T的方程；
（2）是否存在斜率为

的直线l与曲线C交于P、Q两不同点，使得

（O为坐标原点），若存在，求出直线l的方程，否则，说明理由．