题目内容
【题目】已知双曲线![]() 和椭圆
和椭圆![]() 有公共的焦点,且离心率为
有公共的焦点,且离心率为![]() .
.
(Ⅰ)求双曲线![]() 的方程.
的方程.
(Ⅱ)经过点![]() 作直线
作直线![]() 交双曲线
交双曲线![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】试题分析:
(I)设双曲线方程为![]() ,由题意得
,由题意得![]() ,结合
,结合![]() ,可得
,可得![]() ,故可得
,故可得![]() ,
, ![]() ,从而可得双曲线方程。(Ⅱ)由题意知直线
,从而可得双曲线方程。(Ⅱ)由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,与双曲线方程联立消元后根据根与系数的关系可得
,与双曲线方程联立消元后根据根与系数的关系可得![]() ,解得
,解得![]() 可得直线方程。
可得直线方程。
试题解析:
(I)由题意得椭圆![]() 的焦点为
的焦点为![]() ,
, ![]() ,
,
设双曲线方程为![]() ,
,
则![]() ,
,
∵![]()
∴![]() ,
,
∴ ![]() ,
,
解得![]() ,
,
∴ ![]() ,
,
∴ 双曲线方程为![]() .
.
(II)由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,即
,即![]() 。
。
由 消去x整理得
消去x整理得
![]() ,
,
∵直线![]() 与双曲线交于
与双曲线交于![]() ,
, ![]() 两点,
两点,
∴ ,
,
解得![]() 。
。
设![]() ,
, ![]() ,
,
则![]() ,
,
又![]() 为
为![]() 的中点
的中点
∴ ![]() ,
,
解得![]() .满足条件。
.满足条件。
∴ 直线![]() ,即
,即![]() .
.

【题目】2017年春晚分会场之一是凉山西昌,电视播出后,通过网络对凉山分会场的表演进行了调查.调查分三类人群进行,参加了网络调查的观众们的看法情况如下:
观众对凉山分会场表演的看法 | 非常好 | 好 |
中国人且非四川(人数比例) |
|
|
四川人(非凉山)(人数比例) |
|
|
凉山人(人数比例) |
|
|
(1)从这三类人群中各选一个人,求恰好有2人认为“非常好”的概率(用比例作为相应概率);
(2)若在四川人(非凉山)群中按所持态度分层抽样,抽取9人,在这9人中任意选取3人,认为“非常好”的人数记为ξ,求ξ的分布列和数学期望.
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |
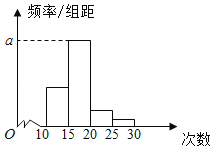
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
【题目】某工厂拟生产甲、乙两种实销产品.已知每件甲产品的利润为0.4万元,每件乙产品的利润为0.3万元,两种产品都需要在A,B两种设备上加工,且加工一件甲、乙产品在A,B设备上所需工时(单位:h)分别如表所示.
甲产品所需工时 | 乙产品所需工时 | |
A设备 | 2 | 3 |
B设备 | 4 | 1 |
若A设备每月的工时限额为400h,B设备每月的工时限额为300h,则该厂每月生产甲、乙两种产品可获得的最大利润为( )
A.40万元
B.45万元
C.50万元
D.55万元
