题目内容
已知函数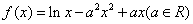 .
.
(Ⅰ)当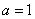 时,证明函数
时,证明函数 只有一个零点;
只有一个零点;
(Ⅱ)若函数 在区间
在区间 上是减函数,求实数
上是减函数,求实数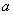 的取值范围.
的取值范围.
解:(Ⅰ)当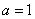 时,
时, ,其定义域是
,其定义域是 ∴
∴ 
令 ,即
,即 ,解得
,解得 或
或 .
.  ,∴
,∴  舍去.
舍去.
当 时,
时, ;当
;当 时,
时, .
.
∴ 函数 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减
上单调递减
∴ 当x =1时,函数 取得最大值,其值为
取得最大值,其值为 .
.
当 时,
时, ,即
,即 . ∴ 函数
. ∴ 函数 只有一个零点.
只有一个零点.
(Ⅱ)显然函数 的定义域为
的定义域为
∴ 
当 时,
时, 在区间
在区间 上为增函数,不合题意
上为增函数,不合题意
当 时,
时, 等价于
等价于 ,即
,即
此时 的单调递减区间为
的单调递减区间为 .依题意,得
.依题意,得 解之得
解之得 .
.
当 时,
时, 等价于
等价于 ,即
,即
此时 的单调递减区间为
的单调递减区间为 ,∴
,∴ 得
得
综上,实数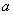 的取值范围是
的取值范围是
法二:
①当 时,
时, 在区间
在区间 上为增函数,不合题意…
上为增函数,不合题意…
②当 时,要使函数
时,要使函数 在区间
在区间 上是减函数,只需
上是减函数,只需 在区间
在区间 上恒成立,
上恒成立,
 只要
只要 恒成立,
恒成立,
 解得
解得 或
或 综上,实数
综上,实数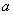 的取值范围是
的取值范围是

练习册系列答案
相关题目
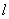 经过点
经过点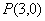 ;倾斜角
;倾斜角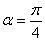 ,
,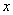 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线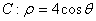 与直线
与直线
 的图象在点
的图象在点 处的切线的倾斜角为( )
处的切线的倾斜角为( ) B.
B. C.
C.  D.
D.
 的定义域为
的定义域为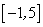 ,部分对应值如下表,
,部分对应值如下表, 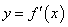 的图
的图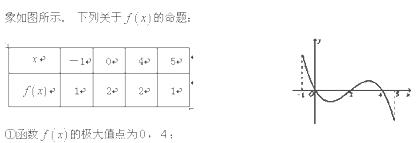
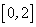 上是减函数;③如果当
上是减函数;③如果当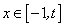 时,
时, 的最大值为4;
的最大值为4;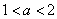 时,函数
时,函数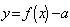 有
有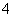 个零点;⑤函数
个零点;⑤函数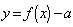 的零点个数可能为0、1、2、3、4个.其中正确命题的序号是
的零点个数可能为0、1、2、3、4个.其中正确命题的序号是  B. -
B. - C.-
C.-
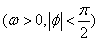 的最小正周期为π,且
的最小正周期为π,且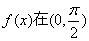 单调递减 B.f(x)在
单调递减 B.f(x)在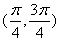 在单调递减
在单调递减 ,则在程序中横线 ? 处应填入语句为( )
,则在程序中横线 ? 处应填入语句为( ) B.
B.  C.
C.  D.
D. 

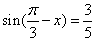 ,则
,则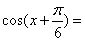
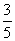 B.
B.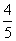 C.
C. D.
D.