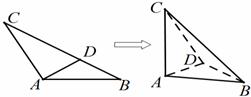
题目内容
如图,已知等腰![]() 的底边
的底边![]() ,顶角为
,顶角为![]() ,
,![]() 是
是![]() 边上一点,且
边上一点,且![]() . 把
. 把![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,连接BC形成三棱锥
,连接BC形成三棱锥![]() .
.
(Ⅰ) ① 求证:AC⊥平面ABD;
② 求三棱锥C-ABD的体积;
(Ⅱ) 求AC与平面BCD所成的角的正弦值.
|
(第20题) |
(Ⅰ) ①由已知得,![]() ,
,![]() .
.
在△ABD中,由BD=1,得AD=![]() =1, 3分
=1, 3分
在△ACD中,∵AC2 + AD2=4 = CD2, ∴AC⊥AD.
平面ADC⊥平面ABD,∴AC⊥平面ABD. 5分
②∵AC⊥平面ABD,
∴VC-ABD=![]() =
=![]() . 8分
. 8分
(Ⅱ) 由![]() ,得CD = 2,
,得CD = 2,
在平面内作等腰△ABC底边上的高线AE,点E为垂足,则AE=![]() .
.
在三棱锥C-ABD中,连接CE,作AH⊥CE于点H,
|
(第20题) |
∵BD⊥AC,BD⊥AE,∴BD⊥平面ACE,
∵AHÌ平面ACE,∴ BD⊥AH,∴AH⊥平面BCD,
∴∠ACH是直线AC与平面BCD所成的角. 11分
在![]() 中,得
中,得![]() ,
,![]() =
=![]() ,
,
∴![]() ,
,
即直线AC与平面BCE所成的角的正弦值为![]() . 14分
. 14分

练习册系列答案
相关题目
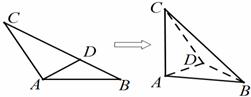
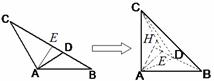
 如图,已知等腰△ABC的底边BC=3,顶角为120°,D是BC边上一点,且BD=1.把△ADC沿AD折起,使得平面CAD⊥平面ABD,连接BC形成三棱锥C-ABD.
如图,已知等腰△ABC的底边BC=3,顶角为120°,D是BC边上一点,且BD=1.把△ADC沿AD折起,使得平面CAD⊥平面ABD,连接BC形成三棱锥C-ABD. 的等腰梯形ABCD,底边BC长为7cm,腰长为
的等腰梯形ABCD,底边BC长为7cm,腰长为 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF= ,试写出左边部分的面积
,试写出左边部分的面积 与
与