题目内容
已知函数f(x)=2x+1,g(x)=x,x∈R,数列{an},{bn}满足条件:a1=1,an=f(bn)=g(bn+1),n∈N*.(1)求证:数列{bn+1}为等比数列;
(2)令cn=
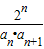 ,Tn是数列{cn}的前n项和,求使Tn>
,Tn是数列{cn}的前n项和,求使Tn>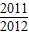 成立的最小的n值.
成立的最小的n值.
【答案】分析:(1)由题意,2bn+1=bn+1,两边同加1,即可证得数列{bn+1}为首项是1,公比为2的等比数列;
(2)求出bn+1=2n-1,可得an=2bn+1=2n-1,对cn=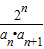 裂项,从而可求Tn的值,利用Tn>
裂项,从而可求Tn的值,利用Tn>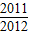 ,即可求得使Tn>
,即可求得使Tn>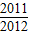 成立的最小的n值.
成立的最小的n值.
解答:(1)证明:由题意,2bn+1=bn+1,
∴2(bn+1)=bn+1+1
∵a1=2b1+1=1,∴b1=0,∴b1+1=1≠0
∴数列{bn+1}为首项是1,公比为2的等比数列;
(2)解:由(1)知,bn+1=2n-1,∴an=2bn+1=2n-1
∴cn=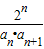 =
=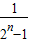 -
-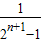
∴Tn=(1- )+(
)+( -
- )+…+(
)+…+(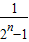 -
-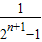 )=1-
)=1-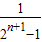
∵Tn>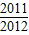 ,∴2n+1>2013,∴n≥10
,∴2n+1>2013,∴n≥10
∴使Tn>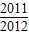 成立的最小的n值为10.
成立的最小的n值为10.
点评:本题考查了等比数列的概念,以及数列的求和的运用.解决该试题的关键是能利用关系式,得到任意相邻两项的关系式,利用定义证明.
(2)求出bn+1=2n-1,可得an=2bn+1=2n-1,对cn=
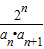 裂项,从而可求Tn的值,利用Tn>
裂项,从而可求Tn的值,利用Tn>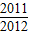 ,即可求得使Tn>
,即可求得使Tn>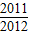 成立的最小的n值.
成立的最小的n值.解答:(1)证明:由题意,2bn+1=bn+1,
∴2(bn+1)=bn+1+1
∵a1=2b1+1=1,∴b1=0,∴b1+1=1≠0
∴数列{bn+1}为首项是1,公比为2的等比数列;
(2)解:由(1)知,bn+1=2n-1,∴an=2bn+1=2n-1
∴cn=
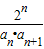 =
=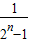 -
-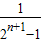
∴Tn=(1-
 )+(
)+( -
- )+…+(
)+…+(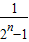 -
-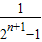 )=1-
)=1-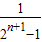
∵Tn>
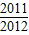 ,∴2n+1>2013,∴n≥10
,∴2n+1>2013,∴n≥10∴使Tn>
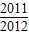 成立的最小的n值为10.
成立的最小的n值为10.点评:本题考查了等比数列的概念,以及数列的求和的运用.解决该试题的关键是能利用关系式,得到任意相邻两项的关系式,利用定义证明.

练习册系列答案
相关题目