题目内容
11.设函数f(x)=x2-2x,g(x)=mx+2,若对任意的x1∈[-1,2],存在x0∈[-1,2],使得g(x1)=f(x0),则实数m的取值范围是( )| A. | [0,$\frac{1}{2}$] | B. | [-1,$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,1] | D. | [0,1] |
分析 作函数f(x)=x2-2x与函数g(x)=mx+2的图象,利用数形结合的思想讨论即可.
解答 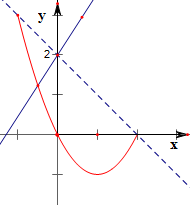 解:作函数f(x)=x2-2x与函数g(x)=mx+2的图象如右图,
解:作函数f(x)=x2-2x与函数g(x)=mx+2的图象如右图,
①当m=0时,g(x1)=2,
故对任意的x1∈[-1,2],存在x0∈[-1,2],使得g(x1)=f(x0)成立;
②当m<0时,2m+2≤g(x1)≤-m+2,
故-1≤2m+2≤-m+2≤3,
解得,m≥-1;
结合选项可知,B正确;
故选B.
点评 本题考查了数形结合的思想应用.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
1.在三角形ABC中,若sinAcosB≤0,则三角形ABC为( )
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 直角三角形 | D. | 钝角三角形或直角三角形 |
2.甲、乙两人同时从寝室到教室,甲一半路程步行,一半路程跑步,乙一半时间步行,一半时间跑步,如果两人步行速度、跑步速度均相同,则( )
| A. | 甲先到教室 | B. | 乙先到教室 | ||
| C. | 两人同时到教室 | D. | 谁先到教室不确定 |