题目内容
已知圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,x轴的正半轴为极轴建立极坐标系,圆
为极点,x轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将圆![]() 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)圆![]() 、
、![]() 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.

【解析】
试题分析:(1)根据曲线![]() 参数方程的形式直接确定圆
参数方程的形式直接确定圆![]() 的圆心与半径,便可求出圆
的圆心与半径,便可求出圆![]() 的普通方程,在圆
的普通方程,在圆![]() 的极坐标方程中,先利用两角和的三角函数公式将等式展开,然后在等
的极坐标方程中,先利用两角和的三角函数公式将等式展开,然后在等 试题解析:(1)由
试题解析:(1)由![]() 得x2+y2=1,
得x2+y2=1,
又∵ρ=2cos(θ+![]() )=cosθ-
)=cosθ-![]() sinθ,
sinθ,
∴ρ2=ρcosθ-![]() ρsinθ.∴x2+y2-x+
ρsinθ.∴x2+y2-x+![]() y=0,
y=0,
即![]() 5分
5分

考点:1.极坐标、参数方程与直角坐标方程之间的转化;2.圆与圆的位置关系;3.公共弦

练习册系列答案
相关题目
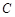 的参数方程为
的参数方程为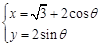 (
( 为参数),若
为参数),若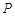 是圆
是圆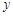 轴正半轴的交点,以坐标原点
轴正半轴的交点,以坐标原点 为极点,
为极点,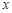 轴的正半轴为极轴建立极坐标系,则过点
轴的正半轴为极轴建立极坐标系,则过点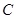 的参数方程为
的参数方程为 (
(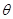 为参数),
为参数),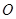 为极点、
为极点、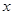 轴的正半轴为极轴建立极坐标系,写出圆
轴的正半轴为极轴建立极坐标系,写出圆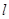 经过原点
经过原点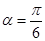 ,设
,设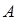 、
、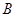 两点,求
两点,求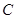 的参数方程为
的参数方程为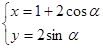 (
(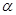 为参数).以原点为极点,
为参数).以原点为极点,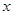 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线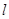 的极坐标方程为
的极坐标方程为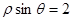 ,则直线
,则直线