Question

【题目】关于函数下列命题错误的是( )

A.函数的图像关于轴对称

B.在区间上，函数是减函数

C.函数的最小值为

D.在区间上，函数是增函数.

Answer 1

【答案】B

【解析】

因为,证明函数的奇偶性和单调性,即可求得答案.

奇偶性证明:

,

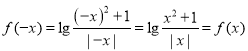
为偶函数

单调性证明:

当时,

根据对数函数单调性可知:单调增函数,

令

当时,根据对号函数图像可知:

当时, 是单调递增;

当时, 是单调递减.

根据复合函数单调性同增异减可知:

当时,是单调递增

当时,是单调递减.

当时,取得最小值,即.

偶函数图像关于轴对称可知:

当时,是单调递减

当时,是单调递增.

综上所述, 对于A,函数的图像关于轴对称,故A正确;

对于B,当时,是单调递减

当时,是单调递增.故B错误;

对于C,函数的最小值为,故C正确;

对于D,在区间上,函数是增函数,故D正确.

故选:B.