题目内容
在等差数列{an}中,a3=6,a5=a2+6.
(1)求数列{an}的通项公式an.
(2)设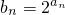 ,判断256是不是数列{bn}的项,若是,为第几项.
,判断256是不是数列{bn}的项,若是,为第几项.
(3)求数列{bn}的前n项和为Tn.
解:(1)设数列的公差为d,则
∵a5=a2+6,∴3d=6,∴d=2
∴an=a3+2(n-3)=2n;
(2)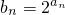 =4n
=4n
令4n=256,∴n=4
∴256是数列{bn}的第4项;
(3)由(2)知,数列{bn}是以4为首项,4为公比的等比数列
∴Tn= =
= .
.
分析:(1)先求出数列的公差,再求数列{an}的通项公式an;
(2)求出数列{bn}的通项,即可求得结论;
(3)利用等比数列的求和公式,可求数列{bn}的前n项和为Tn.
点评:本题考查等差数列的通项,考查等比数列的求和,考查学生的计算能力,属于基础题.
∵a5=a2+6,∴3d=6,∴d=2
∴an=a3+2(n-3)=2n;
(2)
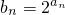 =4n
=4n令4n=256,∴n=4
∴256是数列{bn}的第4项;
(3)由(2)知,数列{bn}是以4为首项,4为公比的等比数列
∴Tn=
 =
= .
.分析:(1)先求出数列的公差,再求数列{an}的通项公式an;
(2)求出数列{bn}的通项,即可求得结论;
(3)利用等比数列的求和公式,可求数列{bn}的前n项和为Tn.
点评:本题考查等差数列的通项,考查等比数列的求和,考查学生的计算能力,属于基础题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目