题目内容
20.在数列{an}中,a1=1,3anan-1+an-an-1=0(n≥2,n∈N).(Ⅰ)试判断数列{$\frac{1}{{a}_{n}}$}是否为等差数列.
(2)求数列{$\frac{2n+5}{{a}_{n}}$}的前n项和.
分析 (I)a1=1,3anan-1+an-an-1=0(n≥2,n∈N).可得$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=3,即可得出.
(2)由(I)可得:$\frac{1}{{a}_{n}}$=1+3(n-1)=3n-2,可得$\frac{2n+5}{{a}_{n}}$=6n2+11n-10,利用12+22+…+n2=$\frac{n(n+1)(2n+1)}{6}$,及其等差数列的前n项和公式即可得出.
解答 解:(I)a1=1,3anan-1+an-an-1=0(n≥2,n∈N).
∴an≠0.
∴$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=3,
∴数列{$\frac{1}{{a}_{n}}$}是等差数列,首项为1,公差为3.
(2)由(I)可得:$\frac{1}{{a}_{n}}$=1+3(n-1)=3n-2,
∴$\frac{2n+5}{{a}_{n}}$=(3n-2)(2n+5)=6n2+11n-10,
∵12+22+…+n2=$\frac{n(n+1)(2n+1)}{6}$,
∴数列{$\frac{2n+5}{{a}_{n}}$}的前n项和=6×$\frac{n(n+1)(2n+1)}{6}$+11×$\frac{n(n+1)}{2}$-10n
=$\frac{n(n+1)(4n+13)}{2}$-10n.
=$\frac{4{n}^{3}+17{n}^{2}-7n}{2}$.
点评 本题考查了结论12+22+…+n2=$\frac{n(n+1)(2n+1)}{6}$及其等差数列的通项公式与前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.某莲藕种植塘每年的固定成本是10000元,每年最大规模的种植量是40000斤,每种值一斤藕,成本增加0.5元,如果收入函数是R(q)=-$\frac{1}{3}$q3+10000q2+$\frac{4020001}{2}$q(q是莲藕的重量,单位:斤),问每年种植( )斤莲藕,可使利润最大.
| A. | 10000 | B. | 12000 | C. | 20000 | D. | 20100 |
11.某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,统计结果如下:
(1)若某企业每天由空气污染造成的经济损失S(单位:元)与空气质量指数API(记为ω)的关系式为:
S=$\left\{\begin{array}{l}0,0≤ω≤100\\ 4ω-400,100<ω≤300\\ 2000,ω>300.\end{array}\right.$试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若以上表统计的频率作为概率,求该城市某三天中恰有一天空气质量为轻度污染的概率.(假定这三天中空气质量互不影响)
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
S=$\left\{\begin{array}{l}0,0≤ω≤100\\ 4ω-400,100<ω≤300\\ 2000,ω>300.\end{array}\right.$试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(2)若以上表统计的频率作为概率,求该城市某三天中恰有一天空气质量为轻度污染的概率.(假定这三天中空气质量互不影响)
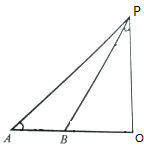 如图,塔PO与地平线AO垂直,在A点测得塔顶P的仰角∠PAO=45°,沿AO方向前进至B点,测得仰角∠PBO=60°,A,B相距44m,求塔高PO(精确到0.1m).
如图,塔PO与地平线AO垂直,在A点测得塔顶P的仰角∠PAO=45°,沿AO方向前进至B点,测得仰角∠PBO=60°,A,B相距44m,求塔高PO(精确到0.1m).