题目内容
已知数列{an}是公差为d(d≠0)的等差数列,Sn为其前n项和。
(1)若a2,a3,a6依次成等比数列,求其公比q;
(2)若 ,求证:对任意的m,n∈N*,向量
,求证:对任意的m,n∈N*,向量 与向量
与向量 共线;
共线;
(3)若 ,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上。
,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上。
(1)若a2,a3,a6依次成等比数列,求其公比q;
(2)若
 ,求证:对任意的m,n∈N*,向量
,求证:对任意的m,n∈N*,向量 与向量
与向量 共线;
共线;(3)若
 ,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上。
,问是否存在一个半径最小的圆,使得对任意的n∈N*,点Qn都在这个圆内或圆周上。 解:(1)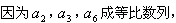
所以,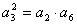 ,即
,即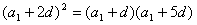 ,
,
解得: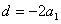 ,∴
,∴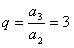 。
。
(2)因为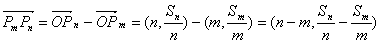 ,
,
而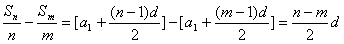 ,
,
所以,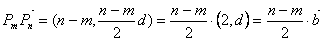 ,
,

(3)因为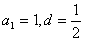 ,
,
所以,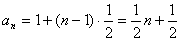 ,
,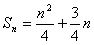 ,
,
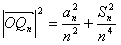
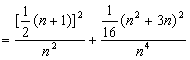
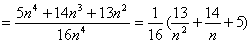 =
=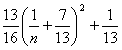 ,
,
因为n≥1,所以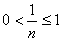 ,
,
∴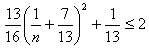 ,当n=1时取等号。
,当n=1时取等号。
所以,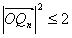 ,即
,即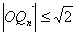 ,
,
所以存在半径最小的圆,最小半径为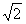 ,使得对任意的n∈N*,点
,使得对任意的n∈N*,点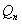 都在这个圆内或圆周上。
都在这个圆内或圆周上。
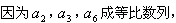
所以,
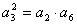 ,即
,即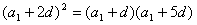 ,
,解得:
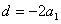 ,∴
,∴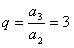 。
。(2)因为
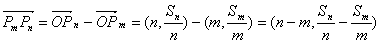 ,
,而
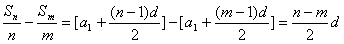 ,
,所以,
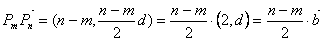 ,
,
(3)因为
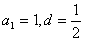 ,
,所以,
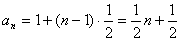 ,
,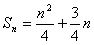 ,
,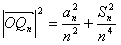
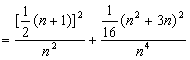
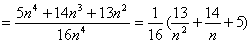 =
=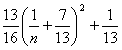 ,
,因为n≥1,所以
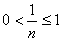 ,
,∴
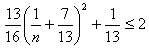 ,当n=1时取等号。
,当n=1时取等号。所以,
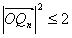 ,即
,即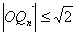 ,
,所以存在半径最小的圆,最小半径为
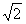 ,使得对任意的n∈N*,点
,使得对任意的n∈N*,点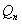 都在这个圆内或圆周上。
都在这个圆内或圆周上。 
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目