Question

如图，已知长方体ABCD-A′B′C′D′中，AB=2

3

，BC=2

3

，AA′=2．
（1）CD和B′D′所成的角是多少度；
（2）BB′和CD′所成的角是多少度．

Answer 1

分析：（1）（2）利用长方体的性质和异面直线所成的角、直角三角形的边角关系即可得出．

解答：解：（1）如图所示．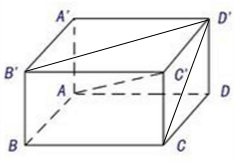
连接B′D′．
由长方体可得：CD∥C′D′．
∴∠C′D′B′即为异面直线CD和B′D′所成的角．
在长方体中，∵AB=BC=2

3

，
∴底面ABCD是正方形，因此A′B′C′D′是正方形．
∴∠C′D′B′=45°．
 （2）连接CD′．
由长方体可得：BB′∥CC′．
∴∠C′CD′是异面直线BB′和CD′所成的角．
在Rt△CC′D′中，
∵CC′=AA′=2，C′D′=AB=2

3

．
∴tan∠C′CD′=

C′D′

CC′

=

3

．
∴∠C′CD′=60°．

点评：本题考查了长方体的性质和异面直线所成的角、直角三角形的边角关系，属于基础题．