题目内容
设全集为R,集M={x| },N={x|
},N={x| },则集合{x|
},则集合{x|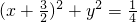 }可表示为
}可表示为
- A.M∪N
- B.M∩N
- C.?RM∩N
- D.M∩?RN
D
分析:由M={x| }={x|
}={x| },可求M,解分式不等式可求,N,进而可求
},可求M,解分式不等式可求,N,进而可求 ,结合选项可判断
,结合选项可判断
解答:由 可得
可得
∴M={x| }={x|-2≤x≤2},
}={x|-2≤x≤2},
∵N={x| }={x|-1<x≤3}
}={x|-1<x≤3}
∴CRM={x|x>2或x<-2}},CRN={x|x>3或x≤-1}
∵{x|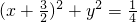 }={x|
}={x| }={x|-2≤x≤-1}
}={x|-2≤x≤-1}
A:M∪N={x|-2≤x≤3},不符题意
B:M∩N={x|-1<x≤2},不符题意
C:CRM∩N={x|2<x≤3},不符题意
D:M∩CRN={x|-2≤x≤-1},符合题意
故选D
点评:本题主要考查了集合的基本运算的应用,解题的关键是根据题意求出相应的集合
分析:由M={x|
 }={x|
}={x| },可求M,解分式不等式可求,N,进而可求
},可求M,解分式不等式可求,N,进而可求 ,结合选项可判断
,结合选项可判断解答:由
 可得
可得
∴M={x|
 }={x|-2≤x≤2},
}={x|-2≤x≤2},∵N={x|
 }={x|-1<x≤3}
}={x|-1<x≤3}∴CRM={x|x>2或x<-2}},CRN={x|x>3或x≤-1}
∵{x|
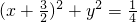 }={x|
}={x| }={x|-2≤x≤-1}
}={x|-2≤x≤-1} A:M∪N={x|-2≤x≤3},不符题意
B:M∩N={x|-1<x≤2},不符题意
C:CRM∩N={x|2<x≤3},不符题意
D:M∩CRN={x|-2≤x≤-1},符合题意
故选D
点评:本题主要考查了集合的基本运算的应用,解题的关键是根据题意求出相应的集合

练习册系列答案
相关题目
 },N={x|
},N={x| },则集合{x|
},则集合{x| }可表示为( )
}可表示为( ) },N={x|
},N={x| },则集合{x|
},则集合{x| }可表示为( )
}可表示为( )