题目内容
函数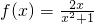 的定义域为
的定义域为 .
.
(1)求函数f(x)的值域;
(2)设函数 .若对于任意x1∈
.若对于任意x1∈ ,总存在x2∈
,总存在x2∈ ,使得g(x2)=f(x1)成立,求a的取值范围.
,使得g(x2)=f(x1)成立,求a的取值范围.
解:(1)求导函数,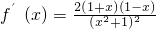 ,∵定义域为
,∵定义域为 ,∴f′(x)>0
,∴f′(x)>0
∴函数在定义域内为增函数,所以函数的值域为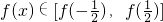 即
即
(2)对函数g(x)求导,得 g′(x)=3(x2-a)
因此 ,当
,当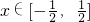 时,g′(x)≤0,所以当
时,g′(x)≤0,所以当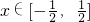 时,g(x)为减函数,
时,g(x)为减函数,
从而当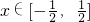 时,有
时,有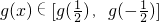
即当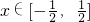 时,
时,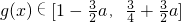
任给x1∈ ,
, ,存在x2∈
,存在x2∈ 使得g(x2)=f(x1),
使得g(x2)=f(x1),
则
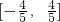
即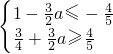 ,结合
,结合  解得
解得 
分析:(1)先求导函数,根据函数的定义域,可知导数大于0,从而函数在定义域内为增函数,所以可求函数的值域;(2)对函数g(x)求导,得 g′(x)=3(x2-a),根据 ,
,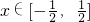 ,可知g′(x)≤0,所以当
,可知g′(x)≤0,所以当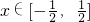 时,g(x)为减函数,从而可求函数g(x)的值域;任给x1∈
时,g(x)为减函数,从而可求函数g(x)的值域;任给x1∈ ,
, ,要使存在x2∈
,要使存在x2∈ 使得g(x2)=f(x1),则函数f(x)的值域是函数g(x)的值域的子集,从而可得结论.
使得g(x2)=f(x1),则函数f(x)的值域是函数g(x)的值域的子集,从而可得结论.
点评:本题以具体函数为载体,考查利用导数确定函数的单调性,考查函数的值域,同时考查存在性问题的求解,其中将函数f(x)的值域是函数g(x)的值域的子集,是解题的关键.
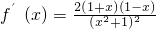 ,∵定义域为
,∵定义域为 ,∴f′(x)>0
,∴f′(x)>0∴函数在定义域内为增函数,所以函数的值域为
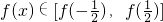 即
即
(2)对函数g(x)求导,得 g′(x)=3(x2-a)
因此
 ,当
,当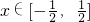 时,g′(x)≤0,所以当
时,g′(x)≤0,所以当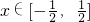 时,g(x)为减函数,
时,g(x)为减函数,从而当
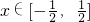 时,有
时,有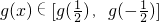
即当
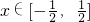 时,
时,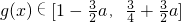
任给x1∈
 ,
, ,存在x2∈
,存在x2∈ 使得g(x2)=f(x1),
使得g(x2)=f(x1),则

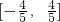
即
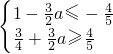 ,结合
,结合  解得
解得 
分析:(1)先求导函数,根据函数的定义域,可知导数大于0,从而函数在定义域内为增函数,所以可求函数的值域;(2)对函数g(x)求导,得 g′(x)=3(x2-a),根据
 ,
,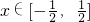 ,可知g′(x)≤0,所以当
,可知g′(x)≤0,所以当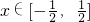 时,g(x)为减函数,从而可求函数g(x)的值域;任给x1∈
时,g(x)为减函数,从而可求函数g(x)的值域;任给x1∈ ,
, ,要使存在x2∈
,要使存在x2∈ 使得g(x2)=f(x1),则函数f(x)的值域是函数g(x)的值域的子集,从而可得结论.
使得g(x2)=f(x1),则函数f(x)的值域是函数g(x)的值域的子集,从而可得结论.点评:本题以具体函数为载体,考查利用导数确定函数的单调性,考查函数的值域,同时考查存在性问题的求解,其中将函数f(x)的值域是函数g(x)的值域的子集,是解题的关键.

练习册系列答案
相关题目
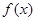
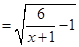 的定义域为集合A,函数
的定义域为集合A,函数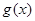
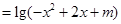 的定义域为集合B
的定义域为集合B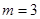 时,求
时,求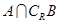
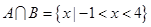 ,求实数
,求实数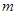 的值
的值 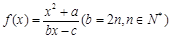 的定义域为{x| x ≠1},图象过原点,且
的定义域为{x| x ≠1},图象过原点,且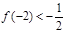 .
.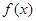 的单调减区间;
的单调减区间;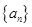 前n项和为
前n项和为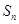 ,满足
,满足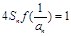 ,
,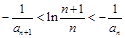 ;
;