题目内容
（2013•德州二模）已知双曲线
-
=1（a＞0，b＞0）的离心率为2，该双曲线与抛物线y2=16x的准线交于A，B两点，若|AB|=6
，则双曲线的方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
分析：根据双曲线方程，求出抛物线的准线方程，利用|AB|=6
，即可求得结论．
| 5 |
解答：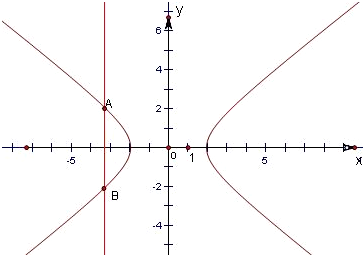
解：∵抛物线y2=16x，2p=16，p=8，∴
=4．
∴抛物线的准线方程为x=-4．
设双曲线与抛物线的准线x=-4的两个交点A（-4，y），B（-4，-y）（y＞0），
则|AB|=|y-（-y）|=2y=6
，∴y=3
．
将x=-4，y=3
．
代入双曲线C：
-
=1，得
-
=1，①
又双曲线
-
=1（a＞0，b＞0）的离心率为2，∴
=2，
即
=4，b2=3a2②
由①②得a2=1，b2=3，
∴双曲线C的方程为x2-
=1，
故选A．
解：∵抛物线y2=16x，2p=16，p=8，∴| p |
| 2 |
∴抛物线的准线方程为x=-4．
设双曲线与抛物线的准线x=-4的两个交点A（-4，y），B（-4，-y）（y＞0），
则|AB|=|y-（-y）|=2y=6
| 5 |
| 5 |
将x=-4，y=3
| 5 |
代入双曲线C：
| x2 |
| a2 |
| y2 |
| b2 |
| 16 |
| a2 |
| 45 |
| b2 |
又双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
即
| a2+b2 |
| a2 |
由①②得a2=1，b2=3，
∴双曲线C的方程为x2-
| y2 |
| 3 |
故选A．
点评：本题考查抛物线，双曲线的几何性质，考查学生的计算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
（2013•德州二模）为了解某校教师使用多媒体进行教学的情况，将全校200名 教师按一学期使用多媒体进行教学的次数分成了[0，9），[10，19），[20，29），[30，39），[40，49）五层．现采用分层抽样从该校教师中抽取20名教师，调查了他们上学期使用多媒体进行教学的次数，结果用茎叶图表示如图，据此可知该校一学期使用多媒体进行教学的次数在[30，39）内的教师人数为