题目内容
已知幂函数f(x)=xα(α为常数)的图象过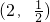 ,则f(x)的单调递减区间是
,则f(x)的单调递减区间是
- A.(-∞,0]
- B.(-∞,+∞)
- C.(-∞,0)∪(0,+∞)
- D.(-∞,0),(0,+∞)
D
分析:利用已知条件先求出α,再利用所求的函数解析式即可得出其单调区间.
解答:∵幂函数f(x)=xα(α为常数)的图象过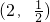 ,
,
∴ ,解得α=-1,
,解得α=-1,
∴幂函数f(x)= .
.
∴f(x)的单调递减区间是(-∞,0),(0,+∞).
故选D.
点评:正确理解函数的单调性是解题的关键.特别注意把单调区间不能写成(-∞,0)∪(0,+∞).
分析:利用已知条件先求出α,再利用所求的函数解析式即可得出其单调区间.
解答:∵幂函数f(x)=xα(α为常数)的图象过
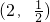 ,
,∴
 ,解得α=-1,
,解得α=-1,∴幂函数f(x)=
 .
.∴f(x)的单调递减区间是(-∞,0),(0,+∞).
故选D.
点评:正确理解函数的单调性是解题的关键.特别注意把单调区间不能写成(-∞,0)∪(0,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目