题目内容
已知集合 ,B={x|x2?m≤0},“x∈A”是“x∈B”的必要条件,求实数m的取值范围.
,B={x|x2?m≤0},“x∈A”是“x∈B”的必要条件,求实数m的取值范围.
解:化简集合A,由 ,配方得
,配方得 ,
,
∵ ,∴当x=
,∴当x= 时,ymin=-1;当x=
时,ymin=-1;当x= 时,ymax=3.
时,ymax=3.
∴y∈[-1,3],∴A={y|-1≤y≤3}.
∵“x∈A”是“x∈B”的必要条件,∴B是A的子集.
化简集合B,①当m<0时,B=∅,∴B⊆A,满足题设.
②当m≥0时,由x2-m≤0得 ,∴
,∴
∵B⊆A,∴ ,解之得0≤m≤1.
,解之得0≤m≤1.
∴实数m的取值范围是(-∞,1].
分析:由二次函数区间的最值可化简集合A,对m分类再由集合的包含关系通过解不等式可得结果.
点评:本题考查集合的包含关系,涉及二次函数区间的最值和分类讨论的思想,属基础题.

练习册系列答案
相关题目
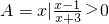 ,B={x|(x+3)(x-a2)≤0}.
,B={x|(x+3)(x-a2)≤0}.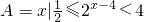 ,B={x|x2-11x+18<0}.
,B={x|x2-11x+18<0}. ,B={x|x2-11x+18<0}.
,B={x|x2-11x+18<0}. ,B={x|(x+a)(x-2a)≤0},其中a>0.
,B={x|(x+a)(x-2a)≤0},其中a>0. ,B={x|m+1≤x≤3m-1}.
,B={x|m+1≤x≤3m-1}.