题目内容
若x1,x2分别为三次函数f(x)=
x3-2x2+3x-5的极大值点和极小值点,则以(x1,0)为顶点,(x2,0)为焦点的双曲线的离心率e 等于______.
| 1 |
| 3 |
求导函数可得f′(x)=x2-4x2+3
令f′(x)=x2-4x2+3>0,可得x<1或x>3;令f′(x)=x2-4x2+3<0,可得1<x<3
∴1,3是函数的极值点
∴(1,0)为双曲线的顶点,(3,0)为双曲线的焦点
∴a=1,c=3
∴e=
=3
故答案为3.
令f′(x)=x2-4x2+3>0,可得x<1或x>3;令f′(x)=x2-4x2+3<0,可得1<x<3
∴1,3是函数的极值点
∴(1,0)为双曲线的顶点,(3,0)为双曲线的焦点
∴a=1,c=3
∴e=
| c |
| a |
故答案为3.

练习册系列答案
相关题目
 .
. ,③
,③
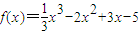 的极大值点和极小值点,则以(x1,0)为顶点,(x2,0)为焦点的双曲线的离心率e 等于 .
的极大值点和极小值点,则以(x1,0)为顶点,(x2,0)为焦点的双曲线的离心率e 等于 .