题目内容
已知数列{an}满足a1=-1，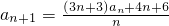
，数列{bn}满足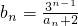
（1）求证：数列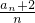
为等比数列，并求数列{an}的通项公式．
（2）求证：当n≥2时，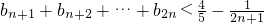
（3）设数列{bn}的前n项和为{sn}，求证：当n≥2时，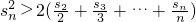
．
解：（1）由题意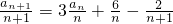
，即
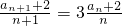
∴an=n•3n-1-2…（4分）
（2）当n=2时，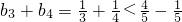
即n=2时命题成立
假设n=k（k≥2）时命题成立，即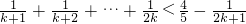
当n=k+1时，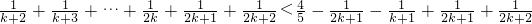
=
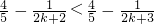即n=k+1时命题也成立
综上，对于任意n≥2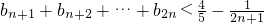，…（8分）
（3）
当n≥2时，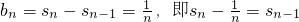
平方则
叠加得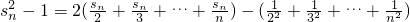
∴
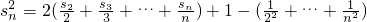
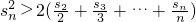∴…（13分）
分析：（1）根据目标，可构造数列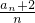，只需对条件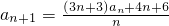进行化简，从而求数列{an}的通项公式．
（2）利用数学归纳法证明，首先证明n=2时命题成立．假设n=k（k≥2）时命题成立，再证明n=k+1时命题也成立
（3）当n≥2时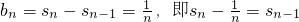，，将其平方，再叠加即可证明．
点评：本题主要考查构造法证明等比数列，从而求出数列的通项，对于不等式的证明由于与自然数有关，故通常可以利用数学归纳法进行证明．
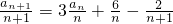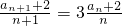
，即∴an=n•3n-1-2…（4分）
（2）当n=2时，
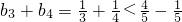即n=2时命题成立假设n=k（k≥2）时命题成立，即
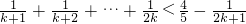
当n=k+1时，
=
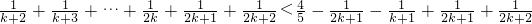
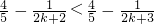即n=k+1时命题也成立综上，对于任意n≥2，
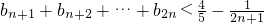…（8分）（3）
当n≥2时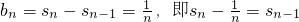，平方则
叠加得
∴
∴
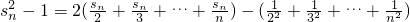
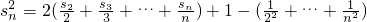
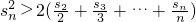…（13分）分析：（1）根据目标，可构造数列
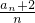，只需对条件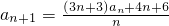进行化简，从而求数列{an}的通项公式．（2）利用数学归纳法证明，首先证明n=2时命题成立．假设n=k（k≥2）时命题成立，再证明n=k+1时命题也成立
（3）当n≥2时，
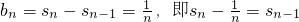，将其平方，再叠加即可证明．点评：本题主要考查构造法证明等比数列，从而求出数列的通项，对于不等式的证明由于与自然数有关，故通常可以利用数学归纳法进行证明．
练习册系列答案
百年学典课时学练测系列答案
相关题目